Någon som kan hjälpa mig med denna uppgift, om integraler

Ser bra ut. Kan du exakt, ej närmevärde,  bestämma värdet av $3\tan (2\cdot\frac{\pi}{8})$?

a) är fel. Derivatan av tangens är något annat. Jag antar att du känner till kvotregeln? Tillämpa den på följande definition av tangens:

$\displaystyle tan\left(x\right)=\frac{sin(x)}{cos(x)}$

dr_lund skrev:

Ser bra ut. Kan du exakt, ej närmevärde,  bestämma värdet av $3\tan (2\cdot\frac{\pi}{8})$?

Nej det är jag osäker på 🤔

moonlighttt skrev:

dr_lund skrev:

Ser bra ut. Kan du exakt, ej närmevärde,  bestämma värdet av $3\tan (2\cdot\frac{\pi}{8})$?

Nej det är jag osäker på 🤔

Kolla i formelsamlingen!

Har gjort den här uträkningen nu, fortsättningen där jag slutade på första bilden på b, ser det rätt ut?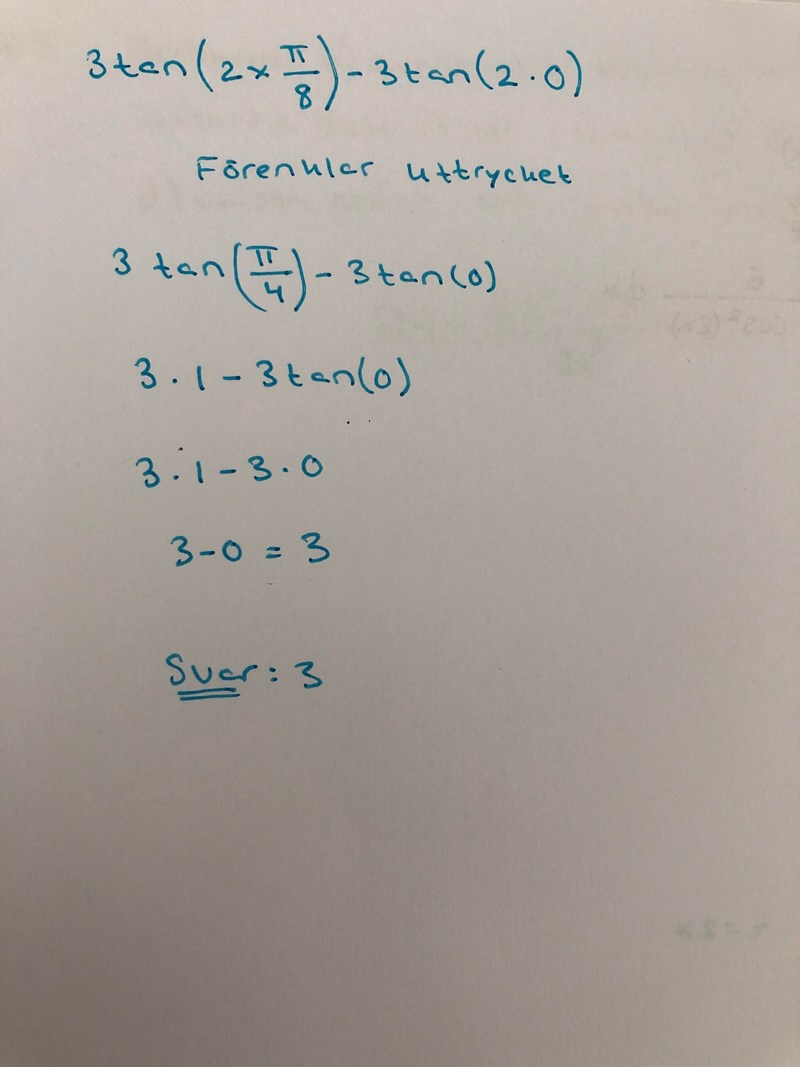

Ebola skrev:

a) är fel. Derivatan av tangens är något annat. Jag antar att du känner till kvotregeln? Tillämpa den på följande definition av tangens:

$\displaystyle tan\left(x\right)=\frac{sin(x)}{cos(x)}$

Har jag tänkt rätt när jag löst den så här?

moonlighttt skrev:

Har gjort den här uträkningen nu, fortsättningen där jag slutade på första bilden på b, ser det rätt ut?

Ja.

Har jag tänkt rätt när jag löst den så här?

Ja.