Någon som kan hjälpa mig vidare, med denna uppgift?

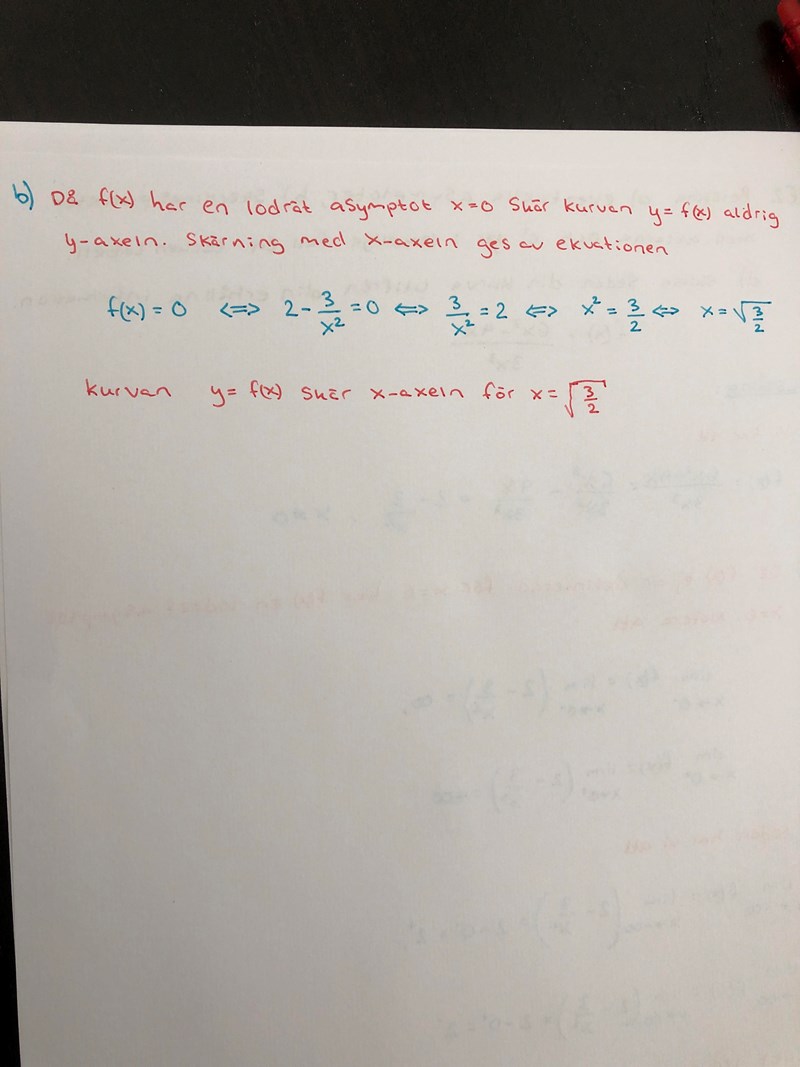
Har du deriverat funktionen och tagit reda på eventuella extrempunkter?

Smaragdalena skrev:

Har du deriverat funktionen och tagit reda på eventuella extrempunkter?

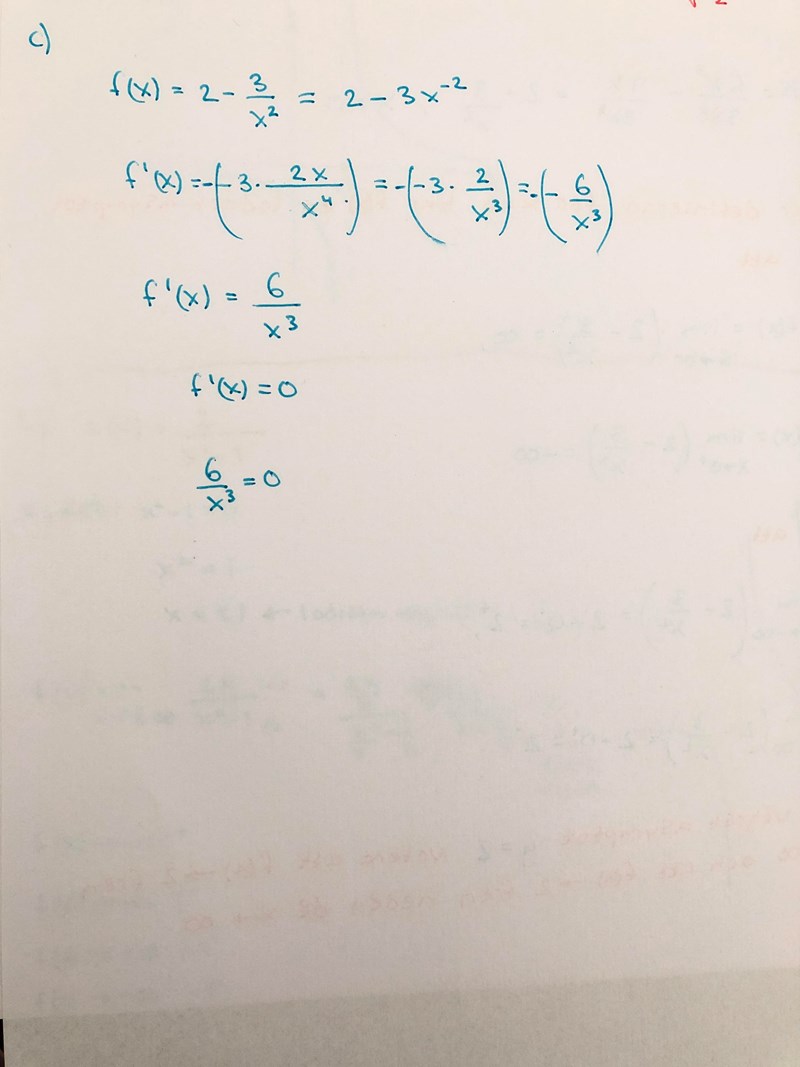Så då behövs det ingen teckentabell för att f(x) >0 för alla x≠0 ? 🤔

Det här stämmer inte:

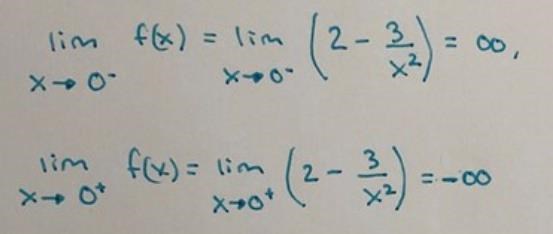
Det enda x:et i uttrycket är kvadrerat, och då blir det ett positivt tal oavsett om det var positivt eller negativt från början. 100^2 blir 10 000, och (-100)^2 blir också 10 000. Så de närmar sig samma oändlighet.

Men det här att tecknet på x inte spelar roll gäller överallt på kurvan, inte bara i detta gränsvärde. Alltså kommer x-värdena 1 och -1 ge precis samma y, 2 och -2 ger samma y, osv. Grafen blir därför helt symmetrisk kring y-axeln, så att vänstra halvan blir liksom en spegling av den högra halvan. Därför kan inte gränsvärdet 2 nås uppifrån i ena fallet och underifrån i andra, grafen måste komma från samma håll på båda sidor. Det är också oroväckande att du får endast ett positivt nollställe - speglingsresonemanget innebär att det då måste finnas ett nollställe på vänstra sidan också.

Skaft skrev:

Det här stämmer inte:

Det enda x:et i uttrycket är kvadrerat, och då blir det ett positivt tal oavsett om det var positivt eller negativt från början. 100^2 blir 10 000, och (-100)^2 blir också 10 000. Så de närmar sig samma oändlighet.

Men det här att tecknet på x inte spelar roll gäller överallt på kurvan, inte bara i detta gränsvärde. Alltså kommer x-värdena 1 och -1 ge precis samma y, 2 och -2 ger samma y, osv. Grafen blir därför helt symmetrisk kring y-axeln, så att vänstra halvan blir liksom en spegling av den högra halvan. Därför kan inte gränsvärdet 2 nås uppifrån i ena fallet och underifrån i andra, grafen måste komma från samma håll på båda sidor. Det är också oroväckande att du får endast ett positivt nollställe - speglingsresonemanget innebär att det då måste finnas ett nollställe på vänstra sidan också.

Nu hänger jag inte med alls, så allt jag gjort i a) och b) är fel då?

"Allt" är väl lite hårt sagt, men helt rätt är det inte. Vad kan jag förtydliga?

moonlighttt skrev:

Nu hänger jag inte med alls, så allt jag gjort i a) och b) är fel då?

Det stämmer att du har en lodrät asymptot vid x = 0 men det stämmer inte att gränsvärdet när x går mot noll från positiva sidan är negativ oändlighet. Vad har det för implikationer för resterande lösning?

Varför har du inte två nollställen för x i b)? Du löser en andragradare men tar bara positiva lösningen.

Finns det någon anledning för dig att inte göra teckentabell? Om du inte vet när du ska göra det och när du inte ska göra det får du ta reda på detta. Förslagsvis bör du ha för vana att alltid göra teckentabell tills du lär dig när det är olämpligt.

Ebola skrev:

moonlighttt skrev:

Nu hänger jag inte med alls, så allt jag gjort i a) och b) är fel då?

Det stämmer att du har en lodrät asymptot vid x = 0 men det stämmer inte att gränsvärdet när x går mot noll från positiva sidan är negativ oändlighet. Vad har det för implikationer för resterande lösning?

Varför har du inte två nollställen för x i b)? Du löser en andragradare men tar bara positiva lösningen.

Finns det någon anledning för dig att inte göra teckentabell? Om du inte vet när du ska göra det och när du inte ska göra det får du ta reda på detta. Förslagsvis bör du ha för vana att alltid göra teckentabell tills du lär dig när det är olämpligt.

Nu har jag försökt lösa om a) och b) ser detta mer rätt ut?

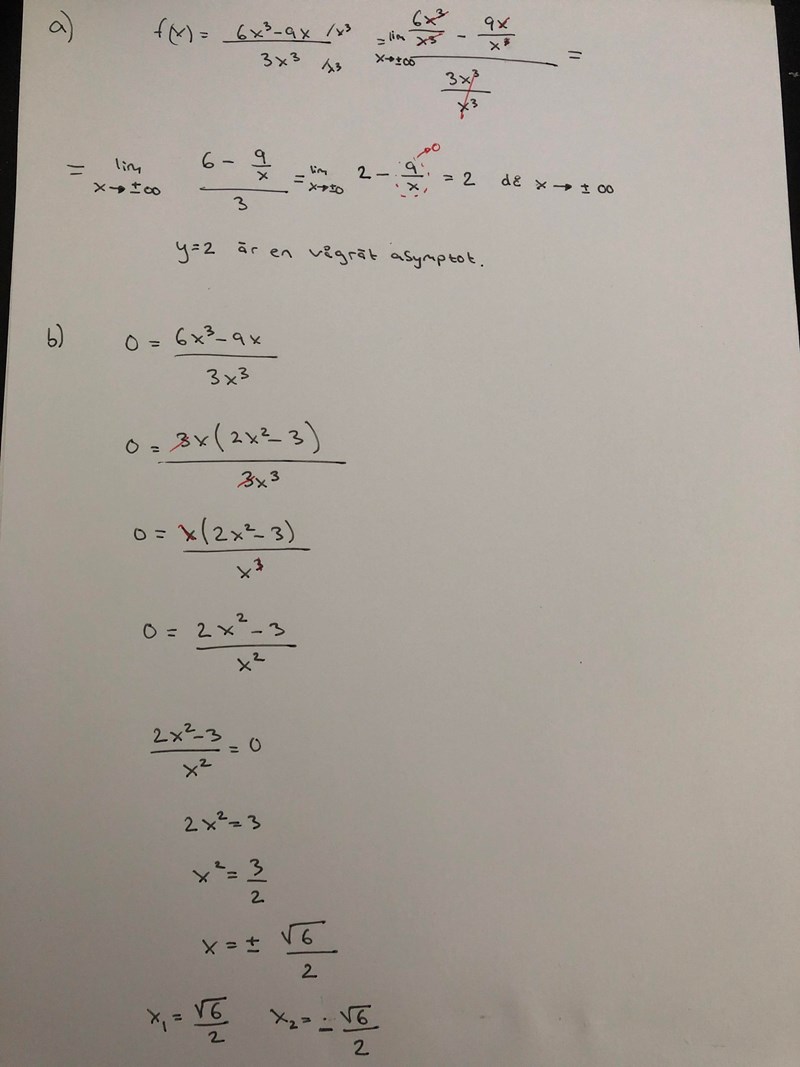
Du hade förenklat funktionen till $f(x) = 2 - \frac{3}{x^2}$ tidigare. Den biten var det inget fel på. Problemet var dina gränsvärden av denna. Prova sätt in små, positiva x-värden där: 0.1, 0.01, 0.001. Vad händer? Prova sedan att sätta in små, negativa x-värden: -0.1, -0.01, -0.001. Vad händer nu?

Skaft skrev:

Du hade förenklat funktionen till $f(x) = 2 - \frac{3}{x^2}$ tidigare. Den biten var det inget fel på. Problemet var dina gränsvärden av denna. Prova sätt in små, positiva x-värden där: 0.1, 0.01, 0.001. Vad händer? Prova sedan att sätta in små, negativa x-värden: -0.1, -0.01, -0.001. Vad händer nu?

Vid positiva x värden blir det ett negativt y värde. Och vid negativa x värden blir det ett positivt y värde 🤔

moonlighttt skrev:

Vid positiva x värden blir det ett negativt y värde. Och vid negativa x värden blir det ett positivt y värde 🤔

Naj, då knappar du nog fel på miniräknaren. 2-3/(-0.001)^2 blir negativt, eftersom i (-0.001) * (-0.001) tar minustecknen ut varann.

Skaft skrev:

moonlighttt skrev:

Vid positiva x värden blir det ett negativt y värde. Och vid negativa x värden blir det ett positivt y värde 🤔

Naj, då knappar du nog fel på miniräknaren. 2-3/(-0.001)^2 blir negativt, eftersom i (-0.001) * (-0.001) tar minustecknen ut varann.

Men förstår inte varför man ska sätta in 0,1 om man ska ta reda på skärningspunkterna så blir dem så som jag har gjort, så då måste b) vara rätt och a) är den som är fel?

Ja, b) ser bra ut i ditt andra försök. Att sätta in små x-värden var bara för att jag ville att du skulle se att kurvan inte går mot $+\infty$ oavsett vilket tecken x har.

Skaft skrev:

Ja, b) ser bra ut i ditt andra försök. Att sätta in små x-värden var bara för att jag ville att du skulle se att kurvan inte går mot $+\infty$ oavsett vilket tecken x har.

Nu har jag försökt klura ut a) ser detta mer rätt ut?

Ja, mycket bättre! Snyggt =)

Skaft skrev:

Ja, mycket bättre! Snyggt =)

Tack för all hjälp 😊tog dock ett tag för mig att lösa den, denna uppgift var svår