När är A(x) konstant?

Att funktionens värde inte förändras även om x förändras. Exempelvis är p(x)=5 en konstant funktion. En egenskap för konstanta funktioner är att dess derivata är 0 överallt. Dessa egenskaper går självklart att även begränsa till intervall alltså om $p(x)=3 \ \forall x \in [0,5]$ så är också derivatan 0 i [0,5].

Men finns det något intervall i för denna graf där derivatan verkligen är för alla x?

Derivatan av A(x) råkar faktiskt vara just f(x) enligt exempelvis analysens huvudsats men du kan också beräkna det själv genom att derivera $\int_0^x f(x)dx=F(x)-F(0)$ där F(x) är en primitiv funktion till f(x).

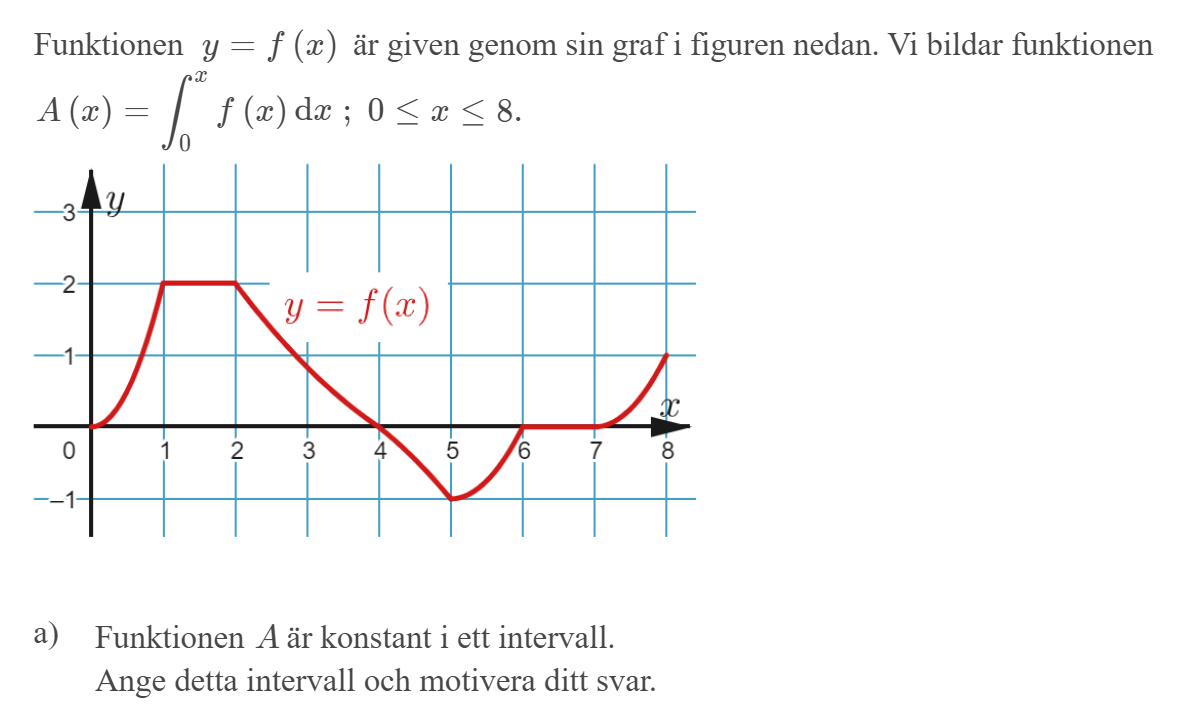
Så det du behöver kolla är för vilka x som f(x) är 0 enligt grafen. Och det är ett litet intervall där om jag inte ser fel. :)

Dvs:

A(x) = F(x) och A'(x) = F'(x) = f(x). f(x) = 0 då 6<x<7?

En fråga också:

Gäller definitionen för en konstant funktion för alla typer av funktioner? Dvs. så fort man hör ordet "konstant funktion" ska man tänka att derivatan = 0. 

Anonym_15 skrev:

Dvs:

 

A(x) = F(x) och A'(x) = F'(x) = f(x). f(x) = 0 då 6<x<7?

Precis, fast A(x)=F(x)-F(0) men F(0) är en konstant som ändå blir 0 vid derivering. 

En fråga också:

Gäller definitionen för en konstant funktion för alla typer av funktioner? Dvs. så fort man hör ordet "konstant funktion" ska man tänka att derivatan = 0. 

Ja, det är ju en egenskap som konstanta funktioner har. Men tänk på att funktionen g(x)=2x ej är konstant, men g'(x)=2 är konstant ty dess derivata g''(x)=0 för alla x.