När borde Linjär Approximation användas?
Här är ett exempel från Lars Filipson då närmevärde kring pi/5 är sökt via det som är känt f(x)=tan x och f(pi/4)=1.

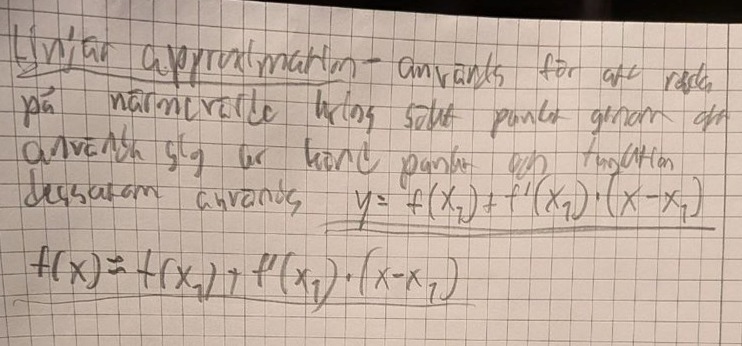
Asså jag tror inte sättet jag skrev på riktigt är rätt, jag kommer ihåg att det fanns en annan ekvation.
Hursomhelst undrar jag:
1. När används den (d.v.s situationer, uppgifter och nivå)?
2. När begränsas den för han sade liksom att "amen pi/4 är hyfsat nära pi/5 så det går att använda linjär approximation". Liksom vad räknas som att det är "nära"?
Den linjära approximationen är bra i en liten omgivning av x_1. Hur bra den är beror på hur stort fel man accepterar. Det här är kanske inledning till Taylor-serier och då kommer uppskattningar av resttermen (felet) in i bilden, men här kankse det bara är en lättsam introduktion. Man approximerar en kurva med dessa tangent. Hur bra denna är beror på var på kurvan man är, hur mycket kurvan kröker sig just i den punkten etc.
Trinity2 skrev:Den linjära approximationen är bra i en liten omgivning av x_1. Hur bra den är beror på hur stort fel man accepterar. Det här är kanske inledning till Taylor-serier och då kommer uppskattningar av resttermen (felet) in i bilden, men här kankse det bara är en lättsam introduktion. Man approximerar en kurva med dessa tangent. Hur bra denna är beror på var på kurvan man är, hur mycket kurvan kröker sig just i den punkten etc.
Ah okej, då får jag börja läsa på om Taylor-serier i sådana fall!

