När kommer Matilda ifatt Lea ?

är det en bra ide att börja ställa hastighterna för både Lea och Matilda ?
Din fråga tyder på att du är osäker på hur du ska ställa upp ekvationen.
Just detta får du stor hjälp med om du börjar med att rita hastighetsgraferna vLea och vMatilda i ett vt-diagram.
Då ser du lättare vilket/vilka samband som måste gälla då Matilda kommer ifatt Lea.
Ok.
Yngve jag har en fråga om jag stöter på liknande uppgifter varför rekommenderar du inte mig att dörska hitta ett uttryck som jag har gjort på matten och lösa uppgiften ? Istället för rita diagram.
Jag tror det har blivit en vana från matten att försöka teckna uttrck och sen lösa uppgiften.
Att rita bilder är inte istället för att sätta upp uttryck och ekvationer.
Du ska teckna uttryck, sätta upp ekvationer och lösa ekvationerna.
Att använda bilder för att illustrera problemet är blott ett tankestöd som hjälper dig att teckna relevanta uttryck och, framför allt, att ställa upp relevanta ekvationer.
Så själva illustrerandet är endast ett förarbete som hjälper dig att lösa rätt problem.
ska jag använda liknande metoder som här https://www.pluggakuten.se/trad/hur-langt-tid-tar-?det-for-a-ar-fore-b/ ?
Förmodligen finns i teoridelen av kapitlet om väg-hastighet-tid härledningar av sträckan s efter tid t med konstant hastighet v (s=vt) och sträckan efter tid med konstant acceleration s=at2/2.
Det är bra att förstå dessa härledningar.
Sen är det här exemplet en "trivial" tillämpning
Arup skrev:ska jag använda liknande metoder som här https://www.pluggakuten.se/trad/hur-langt-tid-tar-?det-for-a-ar-fore-b/ ?
Ja, det tycker jag är en bra idé.
Jag har lite problem med att vt- grafen. Jag vet inte hur kan man rita det på ett bra sätt för att föreställa fenomenet.
Arup skrev:Jag har lite problem med att vt- grafen. Jag vet inte hur kan man rita det på ett bra sätt för att föreställa fenomenet.
Lea cyklar med konstant hastighet. Kan du rita en sådan graf?
Matilda står stilla ett tag och cyklar sedan med konstant acceleration. Kan du rita en sådan graf?
Bubo skrev:Arup skrev:Jag har lite problem med att vt- grafen. Jag vet inte hur kan man rita det på ett bra sätt för att föreställa fenomenet.
Lea cyklar med konstant hastighet. Kan du rita en sådan graf?
Matilda står stilla ett tag och cyklar sedan med konstant acceleration. Kan du rita en sådan graf?
När de menar konstant hastighet tolkar jag det som att jag ska rita en horisontell linje.
Ja, precis. Hastigheten är konstant, dvs den ändras inte. Den är 4.0 m/s vid alla tidpunkter.
Frågan är när kommer Matilda ifatt Lea. Dvs när har du kommit lika långt från en lämpligt vald startpunkt.
För formler se #7
Om vi sätter startpunkten till när Lea först passerar Matilda blir:
För Matilda gäller (observera att hon står still i 2,5 s)
s-t graf för detta: om du sätter kan du beräkna t.
om du sätter kan du beräkna t.
Du får förkasta en av lösningarna då den ligger före Matilda börjar cykla (streckad linje ovanför)
Ok, men varför sa de andra att jag skulle rita vt-graf?
Uppgiften går även att lösa genom att rita två vt-grafer. Du får då två områden: En rektangel för Lea och en triangel för Matilda. Arean av dessa områden motsvarar skillnaden I start- och slutposition för de båda personerna. Eftersom rörelsen sker i en riktning så motsvarar detta tillryggalagd sträcka.
Det som efterfrågas är tidpunkten då dessa tillryggalagda sträckor är lika stora, dvs då areorna är lika stora.
Jag rekommenderar dig att lösa uppgiften på båda sätten. Då ser du att ekvationen du får fram blir identisk i de båda fallen.
Yngve skrev:Uppgiften går även att lösa genom att rita två vt-grafer. Du får då två områden: En rektangel för Lea och en triangel för Matilda. Arean av dessa områden motsvarar skillnaden I start- och slutposition för de båda personerna. Eftersom rörelsen sker i en riktning så motsvarar detta tillryggalagd sträcka.
Det som efterfrågas är tidpunkten då dessa tillryggalagda sträckor är lika stora, dvs då areorna är lika stora.
Jag rekommenderar dig att lösa uppgiften på båda sätten. Då ser du att ekvationen du får fram blir identisk i de båda fallen.
Hur vet du att det blir en rektangel för Lea? Och en triangel för Matilda?
Arup skrev:Yngve skrev:Uppgiften går även att lösa genom att rita två vt-grafer. Du får då två områden: En rektangel för Lea och en triangel för Matilda. Arean av dessa områden motsvarar skillnaden I start- och slutposition för de båda personerna. Eftersom rörelsen sker i en riktning så motsvarar detta tillryggalagd sträcka.
Det som efterfrågas är tidpunkten då dessa tillryggalagda sträckor är lika stora, dvs då areorna är lika stora.
Jag rekommenderar dig att lösa uppgiften på båda sätten. Då ser du att ekvationen du får fram blir identisk i de båda fallen.
Hur vet du att det blir en rektangel för Lea? Och en triangel för Matilda?
Yngve offline så:
Han har läst i uppgiften att Leas hastighet är konstant, samt att Matildas ökar linjärt.
Efter att ha ritat några sådana här grafer så kan man redan utifrån dessa uppgifter se framför sig hur de kommer att se ut.
Prova att rita du också. Det är en nyttig övning. Det är därför Yngve, jag och andra säger ”rita!” så ofta. Man lär sig faktiskt något användbart. (Om inte annat håller du och jag på med annan uppgift just nu där du också skall rita en v/t-graf.)
Jag håller med sictransit här.
Kompletterar med följande minnesregler:
- Vid konstant acceleration så är vt-grafen alltid en rät linje, dvs hastigheten v är en linjär funktion av tiden v(t) = at+v0
- Vid specialfallet konstant hastighet så är vt-grafen en horisontell linje, dvs v(t) = v0 eftersom accelerationen då är lika med 0, dvs a = 0.
=======
Detta hänger intimt ihop med derivatabegreppet som jag hoppas att du sett i dina andra uppgifter:
Accelerationsfunktionen a(t) är derivatan av hastighetsfunktionen v(t), dvs a(t) = v'(t).
Detta ser du även på följande sätt:
I din bok hittar du formeln för hastigheten v som funktion av tiden t vid konstant acceleration a: .v(t) = v0+at., där v0 är ursprungshastigheten och a är accelerationen.
Om du nu deriverar denna funktion med avseende på t så får du v'(t) = 0+a = a, dvs v'(t) = a. Dvs accelerationen är lika med tidsderivatan av hastighetsfunktionen.
Detta är också förklaringen till sambanden att vt-grafen
- har en positiv lutning (positiv derivata) där accelerationen är positiv
- har en negativ lutning (negativ derivata) där accelerationen är negativ
- är horisontell (derivatan = 0) där accelerationen är 0.
======
Hoppas att detta ger dig lite mer sammanhang.
Lite arbetsmaterial från Livehjälpen där Arup och jag diskuterade problemet.
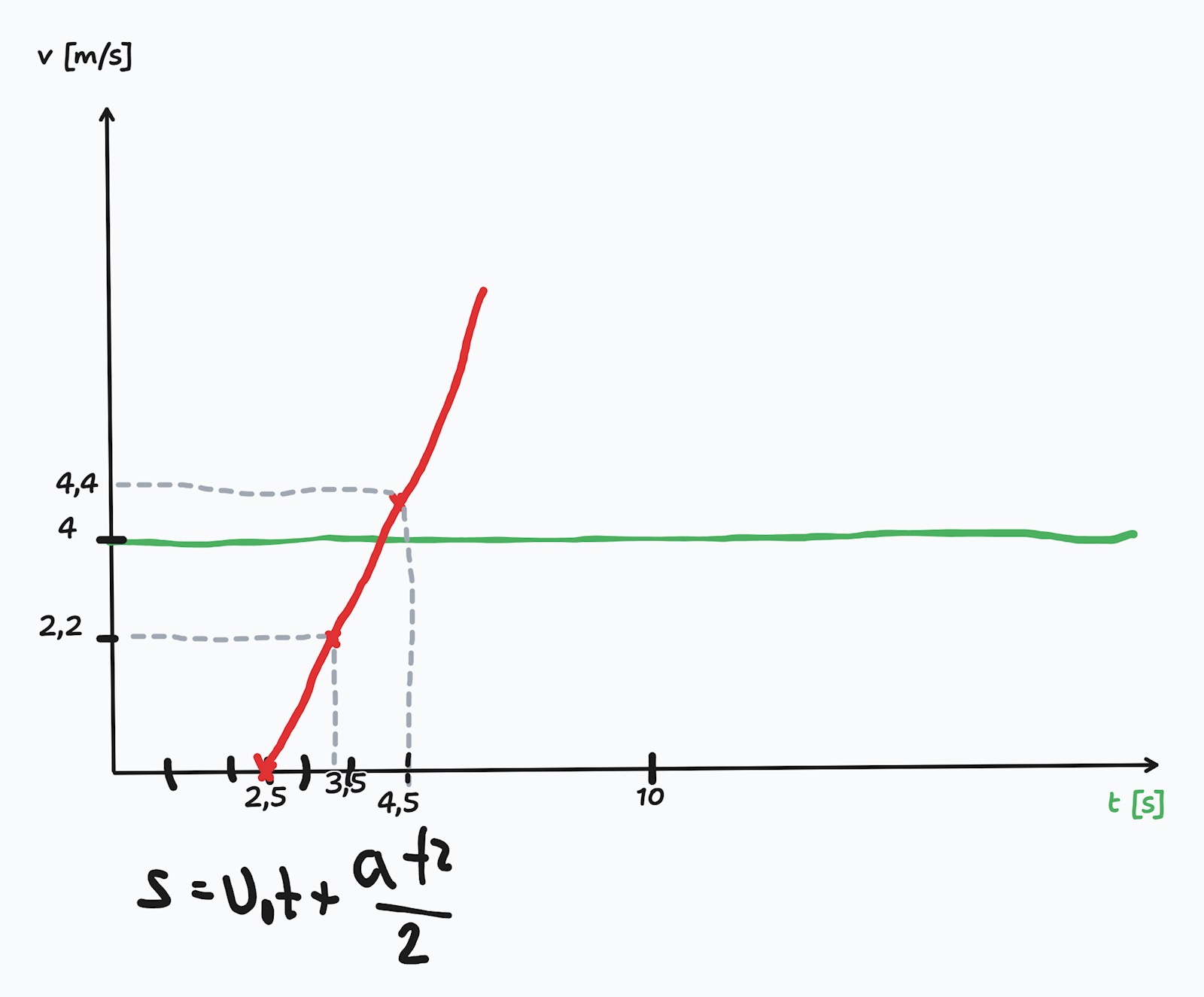

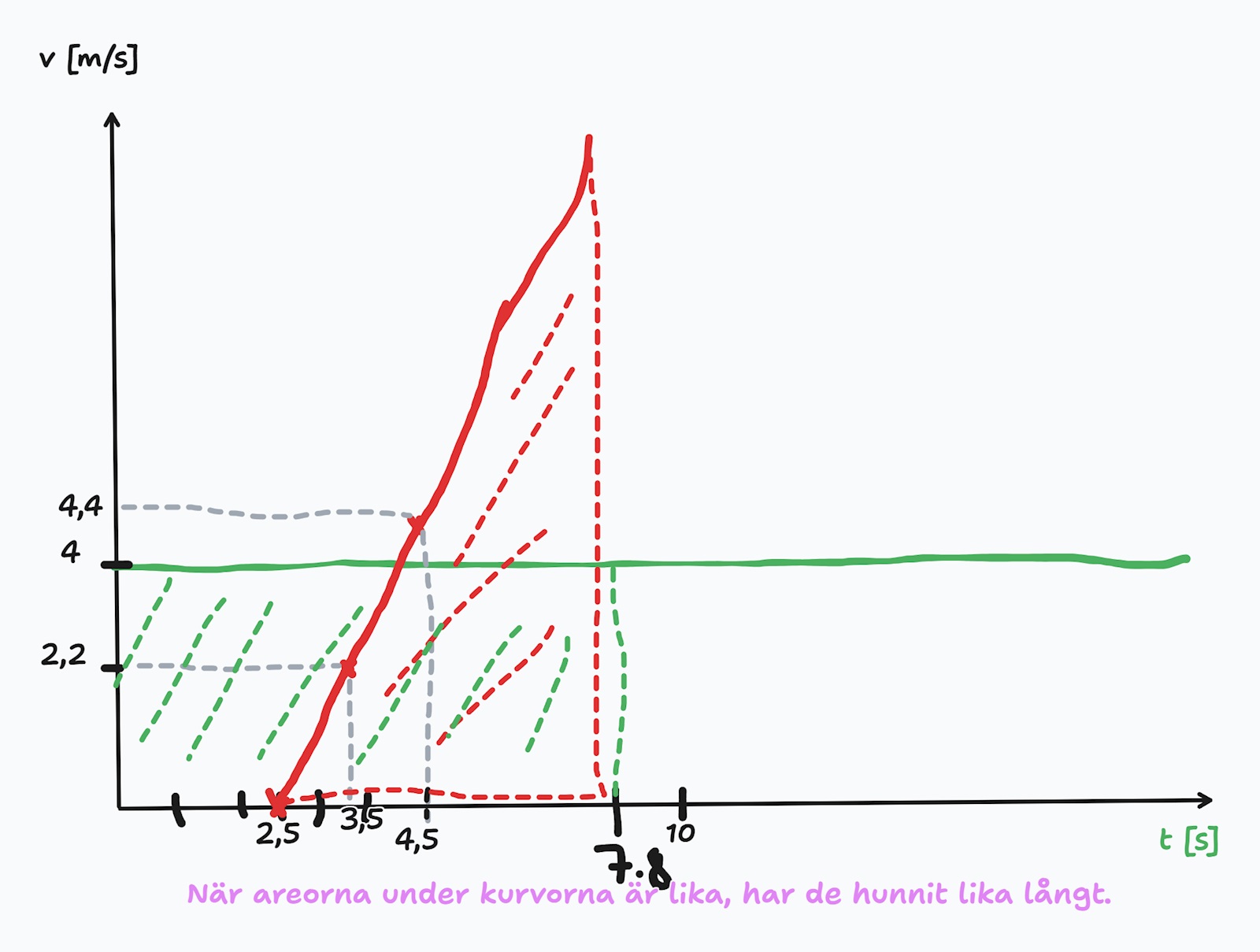
Jag tror det var så Yngve ville ha det.



