NC-svarv
Tyvärr vet jag inte hur man ska tänka. De värden som är inringade i facit skulle jag behöva hjälp med. 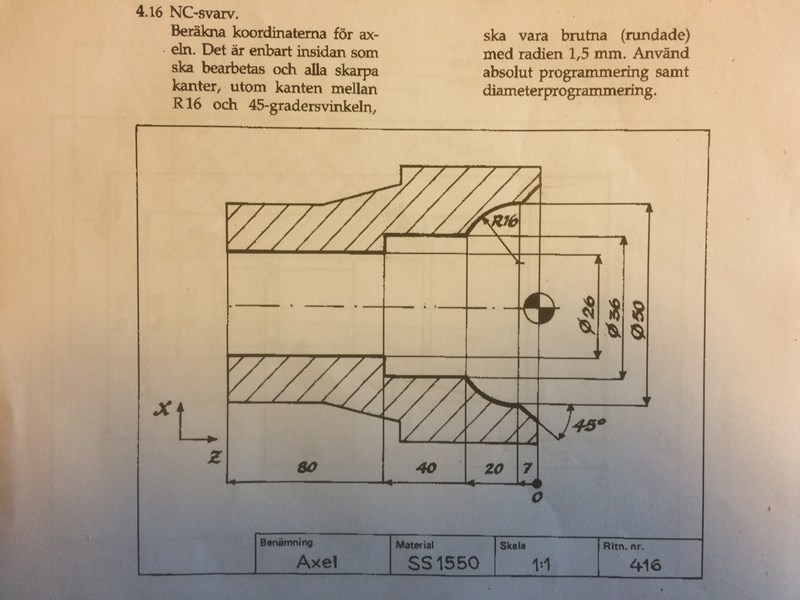
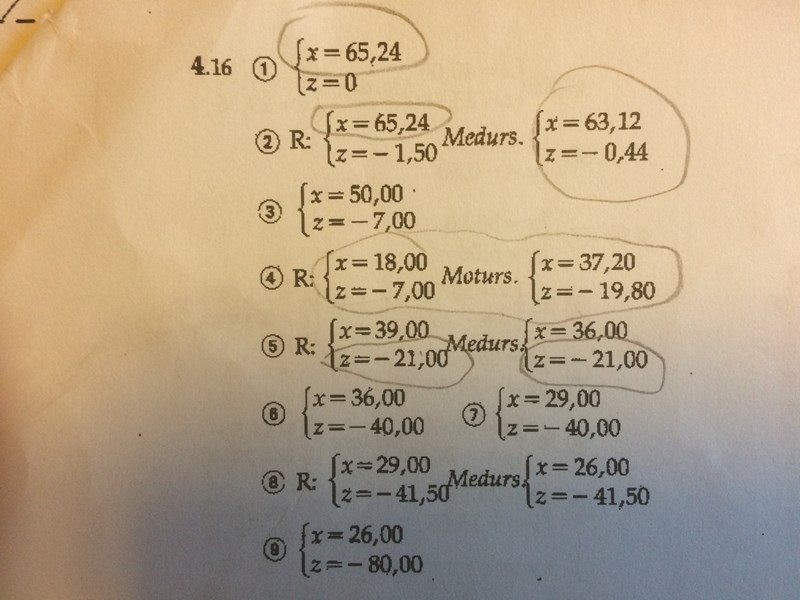
Absolut programmering innebär att alla axlar har samma nollpunkt i koordinatsystemet, hela tiden. Inkremental programmering innebär att nollpunkten allteftersom bearbetningen fortlöper förflyttas till aktuell bearbetningspunkt.
Med diameterprogrammering skrivs x-koordinaterna med sitt dubbla värde. Anledningen till detta förfaringssätt är att ritningsmått oftast är givna som diametermått (inte radiemått). Med detta förfaringssätt blir x-måttet och diametermåttet lika.
Den första punkten är långt till höger och den sista till vänster på bilden.
Den allra största diametern till höger är: 50 + 7 * 2 (önskat diameterprogrammering medför att vi multiplicerar radiemåttet med 2).
Radiemåttet har jag kommit fram till genom:
Tan 45 grader = X / 7
Tan 45 grader * 7 = X (dvs öppning på en valfri sida ger ett större mått än radien 25 (alternativt diametern 50 mm) i storleksordningen som vi beräknar.
X = 7
Med detta följer att största öppningen bör vara 50 + 2 * 7 = 64 mm, innan avrundningen med 1,5 mm. Enligt facit öppnar avfasningen upp hålet med ytterligare 1, 24 mm, men hur?
Jag försöker nu igen med uppgiften 4.16. Nu har jag i alla fall fått fram x-värden för 1 och 2a. När 1,5 mm av 7 mm längst till höger ska vara avfasning, återstår 5,5 mm i z-led som ligger i 45 grader. Jag har kommit fram till att katetrarna i trianglar med 45 graders vinkel och en rät vinkel är lika långa. Därför kan vi utgå från att öppningen genom dessa 5,5 mm på varje sida breddar diametern med totalt 2 * 5,5 mm = 11 mm.
Avfasningen medför att jag ritar en triangel med två katetrar som båda är 1,5 mm och en hypotenusa med okänd längd. Med Pythagoras sats får jag fram längden på hypotenusan: 1,5 i kvadrat + 1,5 i kvadrat = hypotenusan i kvadrat. Tar jag sedan roten ur hypotenusan i kvadrat blir svaret ca 2,12 mm. Eftersom bägge sidorna har samma vinklade öppning utöver yttersta angivna diametern 50 mm ska 2,12 multipliceras med 2 för att innefatta bägge två avfasningarna. Alltså, 2,12 mm * 2 = 4,24 mm.
Totalt breddas 11 mm + 4,24 mm = 15,24 mm. Eftersom diametern är 50 mm innan öppningen som vi räknar på: 50 mm + 15,24 mm = 65,24 mm. Avfasningen har en tänkt mittpunkt för en cirkel 1,5 mm in i z-led, enligt facit till 2a. Denna mittpunkt på samma höjd (x-led) som x för punkt 1 tyder på att fasen (hypotenusan är rundad). Faser är rundade, vet jag av verkstadserfarenhet.
Tyvärr är det nog så att det inte finns någon här på forumet som vet hur man programmerar en NC-svarv, så vi kan inte hjälpa dig.
Ni på forumet kan ju geometri, matematik och trigonometri m.m. Det ni egentligen kan räcker nog många gånger för matematikboken, som jag snart har kommit igenom. Hade jag lagt inläggen under matematik och inte under programmering hade de nog inte sett så avskräckande ut. NC-matematik är enkel i förhållande till teknisk matematik.
För att å fram värden till 2b, provar jag med formeln cos v/2 = (r-h) / r. Det går bra att rätta mig, om ni vet från annat håll att man inte kan göra, som jag gör!
Vinkeln för fasen är 90 grader. Jag ska räkna med halva den vinkeln, dvs 45 grader (cos v/2). Jag önskar få fram höjden utanför de raka linjer, som man kan göra t ex trianglar av inne i cirkeln.
cos 45 grader = (1,5 - h) / 1,5
cos 45 grader * 1,5 = 1,5 - h
h = 1,5 - (cos 45 grader * 1,5)
h = ca 0,44
Där fasen tar slut inne i axeln är där rundningen tar slut och det är i läget x = -0,44
Vi utgick från en radie på 1,5 mm, innan avfasningen. 1,5 - 0,44 = 1,06. Det betyder att 1,06 mm neråt i z-led anger det mått som ska framkomma som z-värde i 2b. Punkten finns i z-led 0,44 mm in i arbetsstycket, där cirkelns höjdsegment har gjort sitt. Eftersom det handlar om diameterprogrammering ska x-värdet dubbleras, för att få fram aktuellt diametermått. Alltså, 65,24 - 2 * 1,06 = 63,12.
2b) x = 63,12
z = -0,44
Jag börjar med x-värdena för 5 a och 5 b, för att kunna lösa resten. 5 b:s x-värde är 36 mm, vilket kan ses på diametermåttet 36. Eftersom det är en avfasning i detta hörn med radien 1,5 och en likadan avfasning på ett ställe till i x-led, multipliceras förändringen i x-led med 2. Detta innebär 1,5 mm * 2 = 3 mm. 36 mm i diametermått (5b) + 3 mm blir 39 mm i x-led (5a).
I föregående kommentar precis här ovanför räknades höjden på cirkelsegmentet ut för avfasningar i storleksordningen 1,5 mm. Höjden på "cirkellocket" är ca 0,44 mm och efter avfasningen återstår 1,5 mm - 0,44 mm av cirkelns ursprungliga radie. Därför lägger jag till 1,06 mm till 5 a:s och 5 b:s z-värde, för att hamna på arbetsstycket och inte i luften. Enligt ritningen är z-värdena för 5 a och 5 b -20 mm, men avfasningen innebär i praktiken att dessa z-värden blir -20 + (-1,06) = ca -21 mm.
Sannolikt bestämmer man sig vid designen, för att placera 4 a grovt räknat en fjärdedel av hela öppningen i axelns högra sida. Om man utgår från 64 mm (innan avfasningen längst ut till höger) innebär detta 18 mm ner från yttre delen av 45-gradersvinkeln. Då är x-värdet för 4a 18 mm och vi kan se på ritningen att punkten ligger på z -7 mm.
De värden som återstår är 4 b; x- och z-värden. Punkten jag söker ska sannolikt placeras utanför avfasningen med radien 1,5 mm, där bågformen åt vänster övergår till en längre sträcka med alltigenom samma x-värde (höjdvärde). Detta är i brytpunkten mellan 20-millimeterspilen under i z-led samt 40 millimeterspilen till vänster. Därför antar jag z-värdet -19,8 för 4 b, som innebär 0,20 mm innan avfasningen börjar.
Sedan gör jag en triangel med radien R16 som på ritningen och ett rakt och lodrätt streck under pilen som pekar mot bågen över R16, en rät vinkel och därifrån ett vågrätt streck till nedre punkten för R16-pilen. Förflyttningen i z-led blir -19,80 - (-7,00), z = 12,80 mm. Med Pythagoras sats räknar jag ut hur lång förflyttningen blir i x-led. 12,80 i kvadrat + x i kvadrat = radien 16 i kvadrat. 16 i kvadrat -12,8 i kvadrat = x i kvadrat, dvs 92,16. Roten ur 92,16 ger x = 9,6 mm.
Eftersom det är diameterprogrammering och ett arbetsstycke som är identiskt på bägge sidor om mittlinjen multiplicerar jag 9,6 med 2 och får 19,2 mm. Jag har x-värdet för den nedre punkten avseende pilen R16 och detta x-värde är 18,00 mm. Lägger jag till 9,6 över 18 och 9,6 neråt får jag diametern 37,2 mm, vilket stämmer med facit för 4 b.
Visst hade jag önskat att jag haft matematiska ögon, för att fastställa siffrorna utan att anta något att utgå ifrån och då välja att anta siffror enligt facit. Om någon kan utläsa exempelvis vinklar för att på så sätt få fram värdena för de två punkterna 4 a och 4 b, eller något annat som går att utläsa av ritningen är jag tacksam...
Här har jag märkt ut punkterna något så när, om det är till hjälp för er.
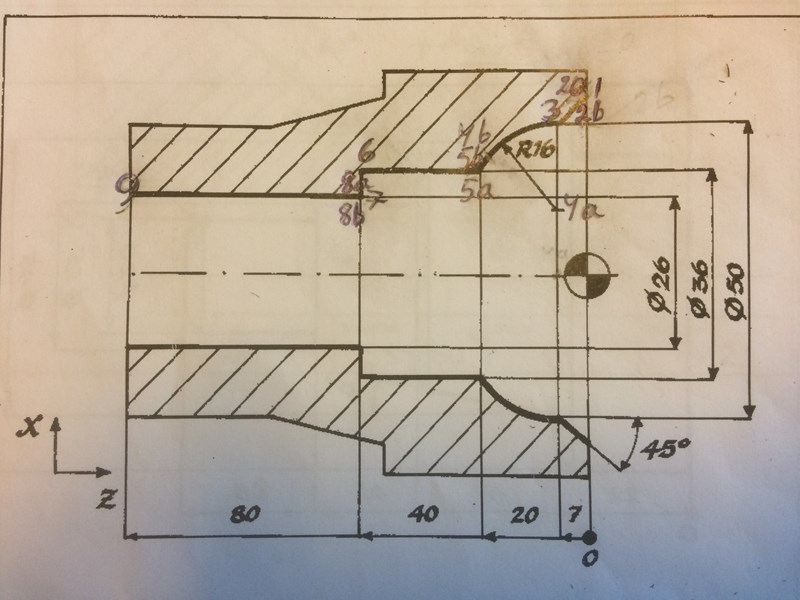
Nyss kom jag på något som gäller inte minst värden för 4 b. Har jag väl fastställt z-led till 12,80 mm har jag 2 sidors längder klara och mer behövs inte för att räkna ut vinklarna i en tänkt triangel. cos vinkeln nere till höger = 12,8 / 16. Vinkeln är ca 36,87 grader. Utgår man från 90 graders vinkel och drar ifrån 36,87 grader kommer man fram till att den andra vinkeln i förbindelsen mellan 4 a och 4 b är 90 - 36,87 grader = ca 53,13 grader.


