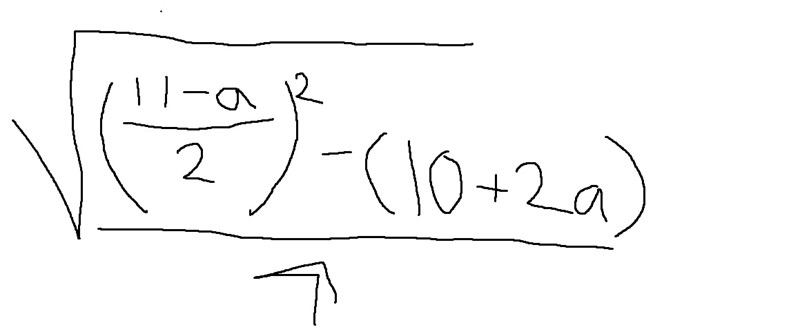Nivå 3 Undersökning av andragradsekvation
Hej, jag har sett denna fråga i några tidigare trådar, men förstår fortfarande inte. Här är frågan: Undersök om ekvationen x2+11x+10 = ax - 2a kan endast ha en rot. Bestäm i så falll värdet av a samt ekvationens lösning.
Jag förstår den biten med att använda pq för att sätta diskriminanten = 0 (för en dubbelrot) Men det jag har problem med är att föra över termerna till en sida av likhetstecknet. Samt hur man löser resten av uppgiften.
(uppskattar all hjälp :) )
För att kunna använda pq-formeln ska vi ha x2+px+q = 0, så för att få vår ekvation på den formen skriver vi om den till
x2 + (11-a)x + (10+2a) = 0.
Är du med så långt?
Så du har faktoriserat (11x-ax). Men varför?
Ahaaa för att få ett p, för det är ju termen framför x
Då är jag med fram dit
Vad blir då diskriminanten?
När är den 0?
Du gav mig den "push-faktor" jag behövde. Fick fram att den är 0 när a =3 , a =27. Skrev in den i den tidigare ekvationen och fick fram x-värderna till ekvationens lösning. Tack så mycket!