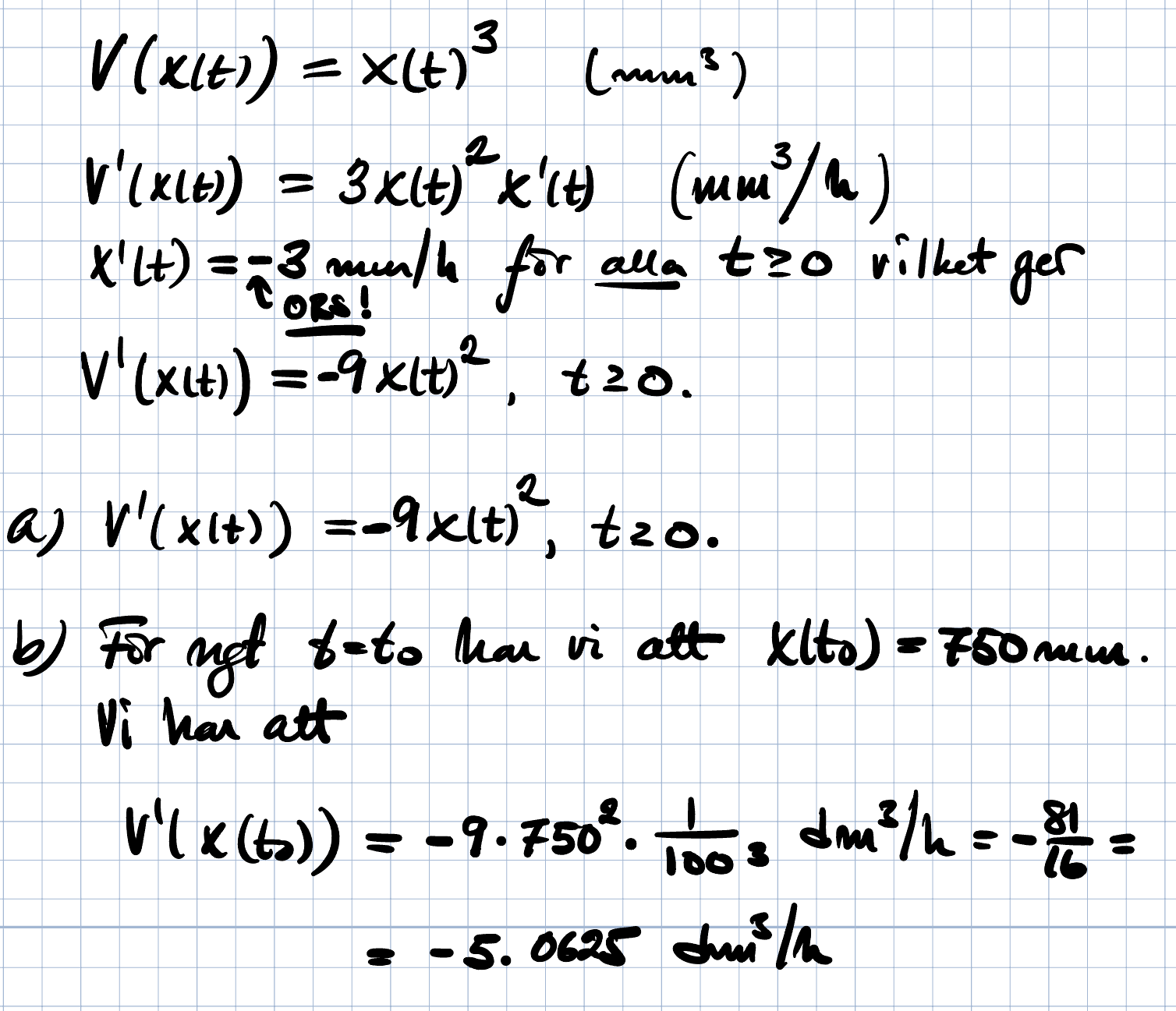Nokflex 2330

Simonload10 skrev:

jag behöver främst förstå hur man kan tolka dV/dx, volym per x? Förstår inte hur vissa derivator ska tolkas och det gör det svårt för mig. När man ska lösa en uppgift som denna, hur bör man då gå till väga?

Man kan tänka täljaren som det som förändras och nämnaren som anledningen till varför det förändras. En vanligt skrivsätt, eller ett sätt man kan tänka på det är: $dV = dV/dx *dx$, alltså en förändringshasighet ($dV/dx$) kommer ge en förändring av V beroende på hur många x som förändras. Alltså, om kubens volym minskar med 10 kubikcentimeter per centimeter som sidan minskar. Och sidan minskar med 3 cm kan vi beräkna volymförändringen $dV$ som $dV = dV/dx *dx = 10 cm^3 / cm * 3 cm = 30 cm^3$. 

Jag betonar det som faktiskt var svaret på din fråga: $dV/dx$ ska tolkas som volymens förändringshastighet, alltså hur snabbt den förändras, med avseende på hur sidan förändras. 

I denna typen av uppgifter kollar man på ett övergripande samband mellan volymen och tiden. "Gömt" inom förändringen är ett beroende av sidlängden som i sin tur är beroende av tiden, som kan vara lättare att räkna på, men framförallt är det angivet i uppgiften. :) 

har jag missförstått variabel x?

Det tror jag inte. Det är kubens sidlängd. Eftersom det är en kub kommer då dess volym bli $x^3$.

Verkar vara något konstigt/bugg med MrPotatoheads inlägg. Det ser ut så här för mig:

men när jag citerar så ser det helt annorlunda ut och det är lättare att förstå (troligen rättat). Kanske ser bra ut för andra?

Ingen skräll att latexen strular här. 

Detta är inlägget.

5,0625 dm3/h

Jag kan intyga om att ungefär 5 kubikdecimeter är korrekt. Dock så behövde man använde minustecknet för att få rätt.

Simonload10 skrev:

Jag kan intyga om att ungefär 5 kubikdecimeter är korrekt. Dock så behövde man använde minustecknet för att få rätt.