Nollställen,funktioner

LittleMissM skrev :

Hur gör jag att uppgifter som ser ut såhär blir lättare att förstå? Jag blir jätte förvirrad när man bara förklarar med bokstäver och siffror. Blir potatismos i huvudet. 

Börja med att faktorisera uttrycket till höger om likhetstecknet. Skriv då först om första termen x^n till x*x^(n-1) så kan du hitta en gemensam faktor i de båda termerna.

Sätt sedan det uttrycket lika med 0. 

Då får du en ekvation som du kan lösa med hjälp av nollproduktmetoden.

 ------

Du kan använda en likande metod på andra uppgiften.

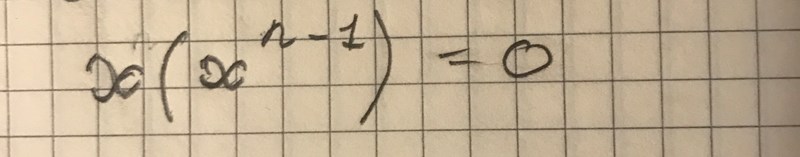
Ska det se ut såhär? 

Kan du förklara nollproduktmetoden till mig lite tydligare. 

Nej det stämmer inte  - multiplicerar du ihop din parentes och ditt x får du inte tillbaka $x^n-n^{n-1}$. Du skall bryta ut faktorn $x^{n-1}$. Vad får du kvar i parentesen?

Om "nånting" gånger "nånting annat" skall bli 0, så måste antingen "nånting" eller "nånting annat" vara lika med 0. I ditt fall måste antingen $x^{n-1}$ eller parentesen ha värdet 0.

Hej!

Uppgift 1046. Välj ett heltal som är större än 1, till exempel heltalet 2. Hur många nollställen har funktionen $y(x) = x^2 - x$? Svar: Två stycken olika nollställen.

Välj ett annat heltal som är större än 1, exempelvis talet 3. Hur många nollställen har funktionen $y(x) = x^3 - x^2$? Svar: Två stycken olika nollställen.

Albiki

LittleMissM skrev :

Hur gör jag att uppgifter som ser ut såhär blir lättare att förstå? Jag blir jätte förvirrad när man bara förklarar med bokstäver och siffror. Blir potatismos i huvudet. 

Ett bra sätt att komma igång är att byta ut n mot ett tal för att få lite enkla exempel. Det lägsta värde n får ha är 2.

Sätt in 2, så får du $y=x^2-x$

Hur många nollställen har den funktionen? Vet du hur du löser $x^2-x=0$

Sedan kan du fortsätta med högre värden på n. Då kanske du ser ett mönster!