Normalfördelninng- vinglas
Livslängden på en viss sorts vinglas är normalfördelat med ett medelvärde på 2 år och en standardavvikelse på 7 månader. En restaurang har precis köpt in 628 nya vinglas. De köper fler vinglas när 100 av dessa har gått sönder. Uppskatta hur många månader det tar innan restaurangen behöver köpa nya glas.
Tycker den var svår. Det jag gjorde var att rita upp en normalfördellnigskurv och skrev ut medelvärde och stardavvikelse. Men vet inte vad det ska hjälpa mig med hur lång tid det tar innan resturangen måste köpa nya glas?
Tråd flyttad från Andragradsekvationer till Statistik. /Smutstvätt, moderator
Etthundra glas måste ha gått sönder, för att de ska köpa nya. Hur många procent motsvarar det?
Smutstvätt skrev:Etthundra glas måste ha gått sönder, för att de ska köpa nya. Hur många procent motsvarar det?
Hur räknar jag ut det? Rita normalfördelningskurva eller?
Nej. Hur många glas köpte de in från början? Hur många hade gått sönder, när de köpt nya?
Smutstvätt skrev:Nej. Hur många glas köpte de in från början? Hur många hade gått sönder, när de köpt nya?
628 nya glas. 100 gick sönder. Vilket är 16% ca?
Precis! De glas som har sämsta kvalitet kommer att gå sönder först. Hur många standardavvikelser fyller dessa 16% av glasen upp? 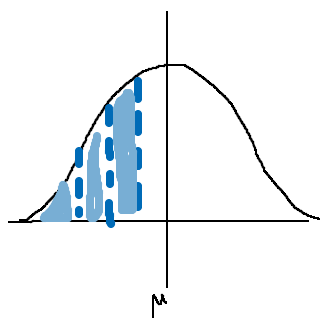
Smutstvätt skrev:Precis! De glas som har sämsta kvalitet kommer att gå sönder först. Hur många standardavvikelser fyller dessa 16% av glasen upp?
hur tar jag reda på det? ska jag använda mig av att medelvärdet är 2 år och en standardavvikelse 7 månader?
Hur många procent ryms inom den nedersta delen? Hur många standardavvikelser kan vi gå upp, innan vi hittar våra 15,9%?

Smutstvätt skrev:Hur många procent ryms inom den nedersta delen? Hur många standardavvikelser kan vi gå upp, innan vi hittar våra 15,9%?
1 standardavvikelse väll?
Från medelvärdet? Korrekt! Hur många månader har de glasen levt?
Smutstvätt skrev:Från medelvärdet? Korrekt! Hur många månader har de glasen levt?
7 månader?
Nja, det är ju en standardavvikelse mindre än medelvärdet, alltså medelvärdet minus sju månader.
AlvinB skrev:Nja, det är ju en standardavvikelse mindre än medelvärdet, alltså medelvärdet minus sju månader.
17? blir det då. Men hur menar du?
Nej, 2 år minus 7 månader, alltså 13 månader.
EDIT: Sjutton månader, inget annat.
Sjutton månader, inget annat.
Smutstvätt skrev:Nej, 2 år minus 7 månader, alltså 13 månader.
Är inte 2år minus 7 månader lika med 17månader? 2år=24månader. 24-7=17?
Men är inte helt med på varför vi tar medelvärdet minus standardavvikelsen.
Ajdå, självklart är det så. Förlåt.
För att de lampor som håller kortast dör först. Vi kan konstatera att eftersom de första hundra glasen måste gå sönder, måste de 15,9 sämsta procenten gå sönder. De fyller ut från vänsterkanten, ända upp till området utanför en (medelvärdet minus en standardavvikelse).
Smutstvätt skrev:Ajdå, självklart är det så. Förlåt.
För att de lampor som håller kortast dör först. Vi kan konstatera att eftersom de första hundra glasen måste gå sönder, måste de 15,9 sämsta procenten gå sönder. De fyller ut från vänsterkanten, ända upp till området utanför en (medelvärdet minus en standardavvikelse).
okej nu förstår jag, tack för hjälpen
Varsågod! :)
Hej! Sry för att jag "stör" i denna tråden, men jag förstår inte hur 13,6 % (en standardavvikelse) kan motsvara ca 16 %. För mig är det mer rimligt att det ligger inom två standardavvikelser (13,6+2,1)%. Skulle någon förklara för mig vad som är fel i tankegången?
Ingen fara! Det är två standardavvikelser, men vi börjar i den ände där glasen har kortast hållbarhetstid. Det medför att när vi fyllt upp våra sexton procent som fick gå sönder, har vi en standardavvikelse kvar till medelvärdet.



