NP-2011 Komplexa tal

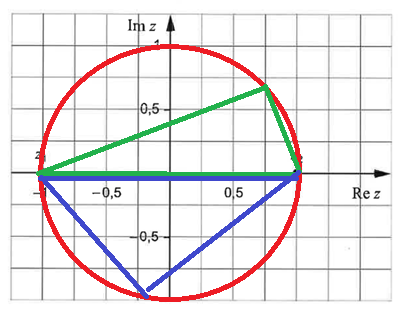
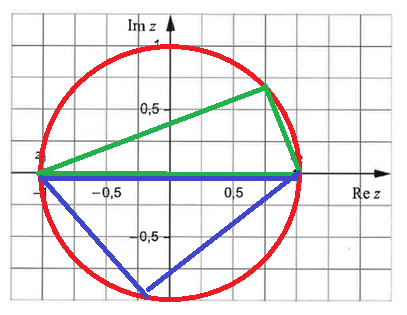
Visa spoiler

Jag förstod inte riktigt vad z3 ska vara? Är det cirkelns ekvation?

Asch!

Jag skulle ha använt Pythagoras. Och fått F ?

AMGOP skrev:

Jag förstod inte riktigt vad z3 ska vara?  

Man tar z₃ = ± i.

Pieter Kuiper skrev:

AMGOP skrev:

Jag förstod inte riktigt vad z3 ska vara?  

Man tar z₃ = ± i.

Hur kan man visa algebraiskt/genrell?

Pieter Kuiper skrev:

AMGOP skrev:

Jag förstod inte riktigt vad z3 ska vara?  

Man tar z₃ = ± i.

Om z3= +- i    bildas ingen rätvinklig triangel?

AMGOP skrev:

Pieter Kuiper skrev:

Visa föregående citat

AMGOP skrev:

Jag förstod inte riktigt vad z3 ska vara?  

Man tar z₃ = ± i.

Hur kan man visa algebraiskt/genrell?

Jag skulle ta Pythagoras, att |z₁ - z₂|² = |z₂-z₃|² + |z₁-z₃|².

Pieter Kuiper skrev:

AMGOP skrev:

Visa föregående citat

Pieter Kuiper skrev:

AMGOP skrev:

Jag förstod inte riktigt vad z3 ska vara?  

Man tar z₃ = ± i.

Hur kan man visa algebraiskt/genrell?

Jag skulle ta Pythagoras, att |z₁ - z₂)² = |z₂-z₃|² + |z₁-z₃)².

Vad betyder denna tecken ) och varför z1- z2? Tack så mycket för dina svar (:

AMGOP skrev:

Pieter Kuiper skrev:

Man tar z₃ = ± i.

Om z3= +- i    bildas ingen rätvinklig triangel?

Jodå: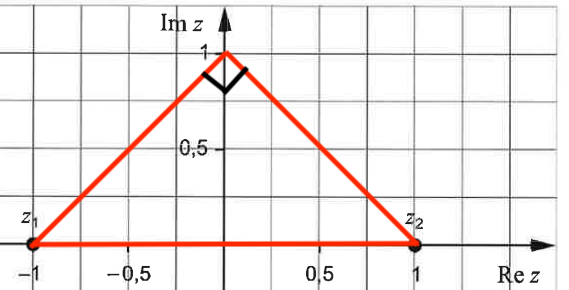

AMGOP skrev:

Pieter Kuiper skrev:

Visa föregående citat

AMGOP skrev:

Pieter Kuiper skrev:

Visa föregående citat

AMGOP skrev:

Jag förstod inte riktigt vad z3 ska vara?  

Man tar z₃ = ± i.

Hur kan man visa algebraiskt/genrell?

Jag skulle ta Pythagoras, att |z₁ - z₂)² = |z₂-z₃|² + |z₁-z₃)².

Vad betyder denna tecken ) och varför z1- z2? Tack så mycket för dina svar (:

Om det ska vara en rät vinkel vid $z_3$ gäller det att distansen mellan $z_1$ och $z_2$ är hypotenusan i triangeln. Distansen mellan två komplexa tal kan beräknas genom att ta absolutbeloppet av deras differens

Pieter Kuiper skrev:

AMGOP skrev:

Visa föregående citat

Pieter Kuiper skrev:

Man tar z₃ = ± i.

Om z3= +- i    bildas ingen rätvinklig triangel?

Jodå:

WOW, tack så mycket, nu jag är med((:

Jag tror dock inte att jag skulle erhållit MVG-kvaliteter för tolkning och utvecklar problem. Suck!

Du kan sätta z₃ var som helst på den här cirkeln med medelpunkt i origo och r=1.

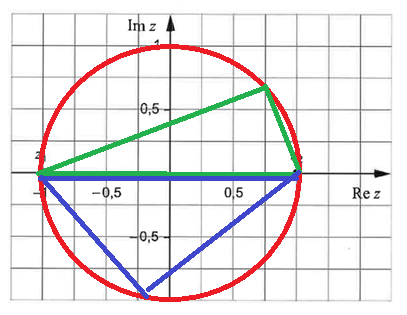
(Ja, kanske inte precis i z₁ eller z₂ då.)

sictransit skrev:

Du kan sätta z₃ var som helst på den här cirkeln med medelpunkt i origo och r=1.

(Ja, kanske inte precis i z₁ eller z₂ då.)

Hur ska man förklara? Alltså hur man har kommit fram till cirkeln? 

Pieter Kuiper skrev:
Jag skulle ta Pythagoras, att |z₁ - z₂|² = |z₂-z₃|² + |z₁-z₃|².

Man kan fortsätta algebraiskt:

$|-1 - 1 |^2 = |1 -z_3 |^2 + |-1-z_3 |^2  \Leftrightarrow$

$4 = |1 -(x+yi)|^2 + |-1 -(x+yi)|^2$

Osv. 

Men bättre med sictransits geometriska lösning. 

Detta följer även från randvinkelsatsen/thales sats 

AMGOP skrev:

sictransit skrev:

Du kan sätta z₃ var som helst på den här cirkeln med medelpunkt i origo och r=1.

(Ja, kanske inte precis i z₁ eller z₂ då.)

Hur ska man förklara? Alltså hur man har kommit fram till cirkeln? 

Det är ett specialfall av randvinkelsatsen. När medelpunktsvinkeln är diagonalen, alltså 180 grader, så är randvinkeln 90 grader.

$z_3=x+iy \mathrm{där} x^2+y^2=1.$