Numeriskderivering , varför ska man ta bort 2:an i nämnaren?

Täljaren har två termer som båda innehåller en faktor 2.
De har brutit ut den faktorn för att sedan förkorta bort den, men de visade inte det räknesteget.
Hur skulle det se ut om man gjorde det steget, förstår inte riktigt hur man kan bryta ut 2:orna i täljaren för att få bort 2 i nämnaren?
moonlighttt skrev:Hur skulle det se ut om man gjorde det steget, förstår inte riktigt hur man kan bryta ut 2:orna i täljaren för att få bort 2 i nämnaren?
Det gäller att
på samma sätt kan man bryta ut i ditt uttryck:
Därefter har du faktorn 2 i både täljare och nämnare, då är det enkelt att förkorta
Så det blir så här, problemet är att jag inte får ut 4 nu som är svaret, eller är det att jag gjort fel i uttrycket ln(2a-2h+1)?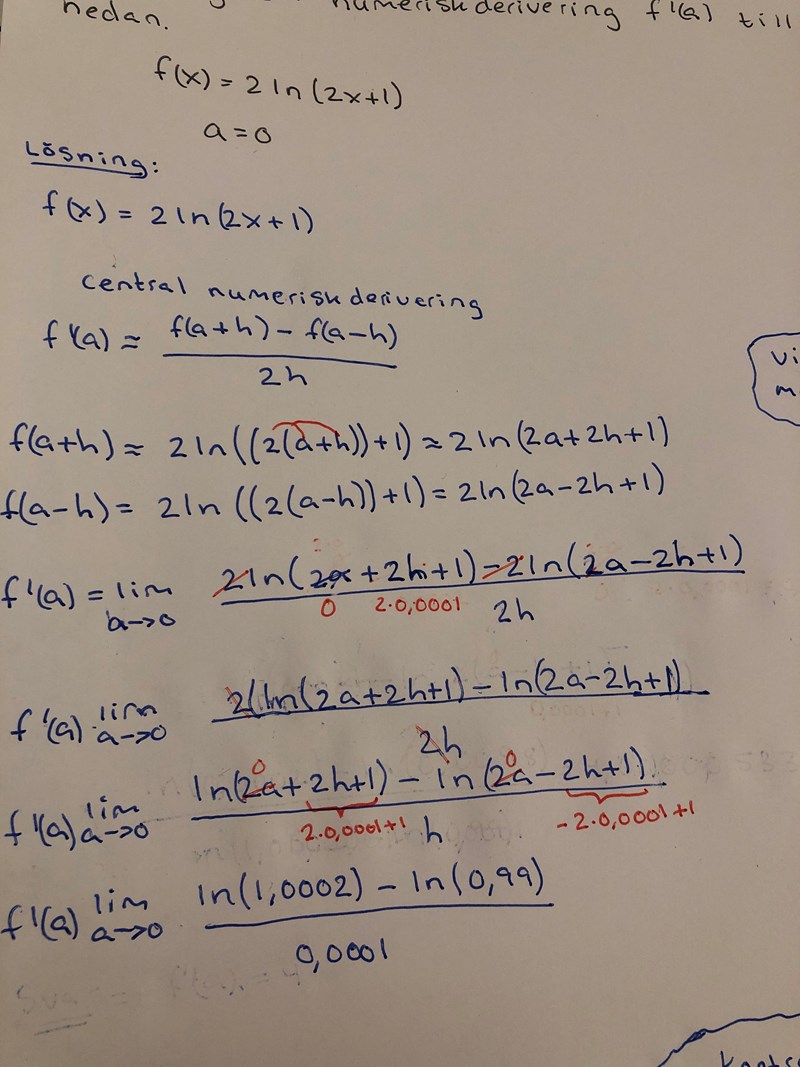
Fick ut att svaret blir 3, om jag skriver in ln(0,9999) inte förkorta det till 0,99, så får ändå ut fel svar
I täljarens andra term ska det vara -2h + 1 = -2*0,0001 + 1 = -0,0002 + 1 = 0,9998.
Avrunda inte.
---------
Sen ska det vara lim h -> 0, inte lim a -> 0.
Plus en del andra skrivfel, som vi inte behöver fördjupa oss i nu.
Jaha okej för vår lärare skrev att h—> kunde ersättas med a—> här för att a=o. Så här skrev han på tavlan, men förstod inte riktigt allt han menade för han skrev båda två under lim Men det är rätt som jag skrivit när jag bröt ut en 2:a för blev osäker nu för då ska jag väll ta bort de andra 2:orna i parantesen?
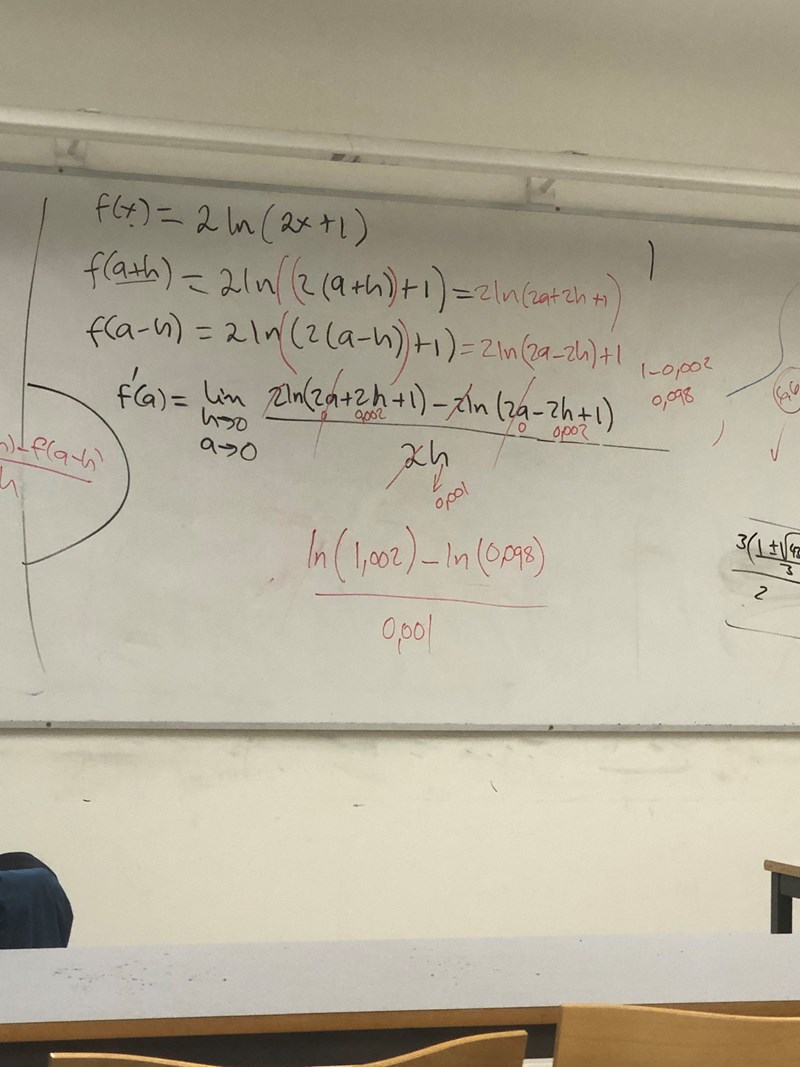
Jag ser ingen anledning att skriva till a -> 0 i uträkningarna. Det går lika bra att helt enkelt ersätta a med 0 i uträkningarna efter att du har ställt upp differenskvoten.
----------
Jag vet inte hur din lärare förklarade det hela, men det är viktigt att skilja på numerisk derivering och äkta derivering.
Numerisk derivering, observera tecknet "ungefär lika med":
Äkta derivering:
Aa okej, då förstår jag tack


