Nya kluringar

Låt cirkeln tangera BC vid E och AC vid F. Sätt AD=x, DB=y, och låt cirkelns radie vara z. AFM är kongruent med ADM (känd egenskap för inskrivna cirkeln: rät vinkel, z och AM gemensamt), och alltså är även AF=x. Pss fås BE=y. Eftersom ACB är rät och CF=CE fås CF=CE=z. 

Triangelns area kan nu beräknas som summan av deltrianglarnas areor:

$A=xz+yz+z^2$

Pythagoras sats för hela triageln ger

$$\begin{gathered} (z+y{)}^2+(z+x{)}^2=(x+y{)}^2 \\ {z}^2+x^2+2xz+y^2+z^2+2yz=x^2+y^2+2xy=x^2+y^2+22 \\ 2z^2+2xz+2yz=22 \\ A=11 \end{gathered}$$

Mycket bra! Har inget att ändra på eller tillägga. Din tur att komma med en ny uppgift.

Låt a,b,c,d vara positiva heltal, sådana att $a^3=b^4, c^5=d^6$. Om b-c=61, vad är a-d?

Positiva heltalspar som uppfyller $a^3=b^4$ är endast $\left(a,b\right)=\left(0,0\right)$ och $\left(1,1\right)$. Talet $b$ kan alltså max vara 1. Jag förstår inte hur 1 minus ett positivt heltal $c$ kan bli 61.

Lirim.K skrev :

Positiva heltalspar som uppfyller $a^3=b^4$ är endast $\left(a,b\right)=\left(0,0\right)$ och $\left(1,1\right)$. 

Det här är inte sant. 1000^4=10000^3. Som exempel.

Just det. Kan man tänka att det är ett ekvationssystem då där

     $$\begin{gathered} \begin{array}{rcl}{a}^3& =& b^4\\ c^5& =& d^6\end{array} \\ b-c=61 \end{gathered}$$

Där vi söker talet $a-d$ ?

593, med brutalmetoden

a = 625

b = 125

c= 64

d = 32

Helt rätt. Men hur brutal var metoden? Gissar att du måste gjort någon ansats.

Värre än så: En liten programsnutt, jag vet att det är fusk, men det underlättade...

medan du funderar på om du godkänner min metod  så lägger jag i en en ny kluring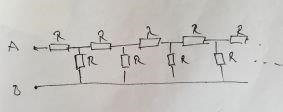

Ett oändligt resistansnät enligt figuren, varje resistor har resistansen R, vilken resistans känner man mellan A och B i figuren?

Tar man bort de två vänstersta motstånden (ett "vågrätt" och ett "lodrätt") så får man kvar exakt samma koppling.

Totalmotståndet X är alltså samma som R i serie med (X och R parallellt).

X = R + RX/(R+X)

Detta ger en andragradsekvation med lösningen X = (1+sqrt(5))/2 * R  

Den andra lösningen ger X<0, ofysikaliskt.

Lägg märke till gyllene snittet!

Vi bör i fortsättnignen vänta tills problem postaren har godkänt lösningen. Det blir rörigt i tråden annars med inlägg som kommer i blandad ordning.

Gyllene snittets kedjebråk 1/1+1/1+1/1+1/... Alla algebraiska tal kan skapas med ettohmsresistorer och mycket kopplingstråd!

Ture: Jag godkänner såklart lösningen. Men elegantare:

Om $b^4$ är en tredjepotens så är även $b$ en tredjepotens (eftersom en primtalsfaktor som förekommer k ggr i b förekommer 4k ggr i b^4; $4k \equiv 0\iff k\equiv 0 (mod 3)$). Sätt $b=u^3$. Motsvarande är $c=v^3$

$61=u^3-v^3=(u-v)(u^2+uv+v^2)$

Eftersom 61 är ett primtal måste u-v=1, och ekvationen blir efter insättning av v=u-1 och förenkling

$$\begin{gathered} u^2-u=20 \\ u=5 \\ v=4 \end{gathered}$$

vilket leder till svaret.

En mycket elegantare lösning än min brutala.

Samtidigt godkänner jag bubos lösning och ber ödmjukt om ursäkt för minbrådska att slänga ur mig en ny uppgift. 

Bubo har alltså inititativet.

Man har tillgång till en balansvåg och ett antal balansvikter. Balansvikterna är heltal.

Uppgiften är att kunna mäta upp alla möjliga mätvärden 0, 1, 2, 3, 4, 5, 6, ..., T-1, T med ett lämpligt urval balansvikter.

Trivialt exempel: Med balansvikterna 1, 2, 4, 8, 16, 32 kan man lätt mäta alla vikter i mätområdet [0, 1, 2, 3, ..., 62, 63].

1) Hur många balansvikter behövs för mätområdet [0, 1, 2, 3, ..., 39, 40]?

2) Allmän lösning? Hur väljer man sina balansvikter optimalt?

EDIT: Det blir lite halvknepigt med ordvalet. Man mäter vikt genom att lägga balansvikter i vågskålarna.

Man kan göra ansättnignen $a^3=b^4=m^{12}$ och $c^5=d^6=n^{30}$. Lite potenslagar ger

     $\begin{array}{rcl}a=m^4& ,& b=m^3\\ c=n^6& ,& d=n^5\end{array}$

Alltså $b-c=61\iff m^3-n^6=61.$ Använder vi kubregeln så kan vi skriva om allt till

     $\left(m-n^2\right)\left(m^2+m{n}^2+n^4\right)=61.$

Det gäller att $m-n^2<m^2+m{n}^2+n^4$ och eftersom 61 är ett primtal så kan den bara faktoriseras om en av parenteserna är lika med ett. Den vänstra parentesen måste vara lika med ett och man får då att

     $m-n^2=1\iff m=1+n^2.$

Insättning i höger parentes ger att

     ${\left(n^2+1\right)}^2+\left(n^2+1\right)n^2+n^4=60\iff 3n^4+3n^2-60=0\iff n^4+n^2-20=\left(n^2-4\right)\left(n^2+5\right)=0.$    

Eftersom $n$ är ett positivt tal så är den enda uppfyllande roten till ekvationen ovan

     $n^2-4=\left(n-2\right)\left(n+2\right)=0\iff n=2.$

Det ger att $m=n^2+1=2^2+1=4+1=5$ som i sin tur ger att

     $\left\{\begin{array}{ll}a=& m^4=5^4=625\\ d=& n^5=2^5=32\end{array}\right.$

och slutligen $a-d=625-32=593.$

1,3,9,27 kan väga allt till och med 40. Trepotenserna är effektivast.

Henrik Eriksson skrev :

1,3,9,27 kan väga allt till och med 40. Trepotenserna är effektivast.

Men då behövs det ju 7 vikter (2 st av 1, 3 och 9 samt 1 st 27).

Med 1, 2, 4, 8, 16, 32 räcker det med 6 vikter.

Henrik Eriksson skrev :

Trepotenserna är effektivast.

Nej, inte i den allmänna lösningen.

Yngve skrev :

Henrik Eriksson skrev :

1,3,9,27 kan väga allt till och med 40. Trepotenserna är effektivast.

Men då behövs det ju 7 vikter (2 st av 1, 3 och 9 samt 1 st 27).

Med 1, 2, 4, 8, 16, 32 räcker det med 6 vikter.

1+3+9+27 = 40

Bubo skrev :

Yngve skrev :

Visa föregående citat

Henrik Eriksson skrev :

1,3,9,27 kan väga allt till och med 40. Trepotenserna är effektivast.

Men då behövs det ju 7 vikter (2 st av 1, 3 och 9 samt 1 st 27).

Med 1, 2, 4, 8, 16, 32 räcker det med 6 vikter.

1+3+9+27 = 40

Ja, men det behövs då ändå 7 vikter för att kunna väga hela intervallet [0, 1, 2... 40]. Hur väger du annars 26?

27 i ena vågskålen och 1 i den andra. Känns  uppgiften lättare eller svårare nu?

n vikter kan placeras på n^3 sätt (vänster , höger, bordet) och på grund av symmetri blir det högst intervallet -(n^3-1)/2 ... +(n^3-1)/2 som täcks. Och med trepotensvikter täcks detta intervall så ingen lösning kan vara bättre.

Bubo skrev :

27 i ena vågskålen och 1 i den andra. Känns  uppgiften lättare eller svårare nu?

Ja! Såklart!

Tänkte inte på att man fick lägga vikter i båda vågskålarna.

Henrik Eriksson skrev :

n vikter kan placeras på n^3 sätt (vänster , höger, bordet) och på grund av symmetri blir det högst intervallet -(n^3-1)/2 ... +(n^3-1)/2 som täcks. Och med trepotensvikter täcks detta intervall så ingen lösning kan vara bättre.

Briljant lösning, måste jag erkänna.

Min lösning är rekursiv: Om man kan väga alla vikter upp till M, så är bästa tänkbara val av nästa vikt (2M+1). Då kan man ju lägga den i ena vågskålen och övriga i andra vågskålen för att väga M+1. Sedan kan man flytta över efterhand, så att man täcker in alla värden upp till 3M+1.

Med den rekursiva lösningen kommer man fram till att vikterna skall vara 1, 3, 9, 27, 81, ...   :-)

Din tur, Henrik!

Med slantsingling kan man som bekant göra ett val med sannolikheten 1/2. Om man får singla flera gånger kan man göra ett val med sannolikheten 1/3. Hur? Och hur är metoden att göra ett val med irrationell sannolikhet, till exempel 0,14159265358979323846264338327950288419716939937510...

Om man vill ha tex sannolikheten 1/5 kan man ju använda en 6 sidig tärning och bara förkasta alla gånger man får 6. Alla andra utfall har då en sannolikhet på 1/5. Att man ibland får 6 påverkar ju inte sannolikheten, det är helt enkelt utfall som inte räknas.

På samma sätt kan du med ett mynt få 1/3 genom att kasta 2 ggr och tex förkasta alla klave+klave, de andra utfallen får då 1/3.

Om man vill kunna få en irrationell sannolikhet kan man använda 4 kast för varje decimal och se utfallen som ett binärt tal (klave=0, kroba=1). Man får bara förkasta 101* och 11*.

Ingen snygg lösning, men det borde ge ett korrekt resultat.

Rätt, men det är inte den bästa lösningen. I båda fallen finns det metoder som kräver färre kast i snitt och som dessutom är enklare.

Om vi tar det här med slantsinglingen så kommer ett förslag här:

För fördelningskonverterigen gäller att på något listigt sätt kombinera 2 potenser så att det till slut blir en tredjedel.

Om vi då använder För-första-gången fördelningen se https://sv.wikipedia.org/wiki/Geometrisk_f%C3%B6rdelning

Den är för övrigt omnämnd i en tidigare kluring.

Så om vi då tar och kastar myntet så får vi:
Sannolikhet för första krona i kast nr 1: P(X=1) = 0,5
Sannolikhet för första krona i kast nr 2: P(X=2) = 0,25
Sannolikhet för första krona i kast nr 3: P(X=3) = 0,125
Sannolikhet för första krona i kast nr 4: P(X=4) = 0,0625
Sannolikhet för första krona i kast nr 5: P(X=5) = 0,03125
Sannolikhet för första krona i kast nr 6: P(X=6) = 0,015625
osv.

Summan av sannolikheterna är en geometrisk serie med k=0,5 och summan 0,5/(1-0,5)=1
Summan av sannolikheterna för första krona i jämna kast nr är 0,25/(1-0,25) = 1/3
Summan av sannolikheterna för första krona i udda kast nr är 0,50/(1-0,25) = 2/3

Coolt.
Hur använder man detta i praktiken?
Du skall slumpvis välja mellan A,B och C och har ett mynt. Hur gör du?

Låt A vara tredjedelen, och låt B&C dela på andra 2/3:

Om första kronan är i ett jämt kast -> A. Om första kronan i ett udda kast, singla igen. Om krona -> B, om klave -> C

haraldfreij skrev :

Låt A vara tredjedelen, och låt B&C dela på andra 2/3:

Om första kronan är i ett jämt kast -> A. Om första kronan i ett udda kast, singla igen. Om krona -> B, om klave -> C

Och om det blir klave i första kastet kastar men igen?

Ja, man börjar med att kasta tills man får en krona. Får man det i kast 2 eller 4 eller 6 eller 8... så blir resultatet A.

Ganska snygg princip, men det kan bli rätt många klave i början. Jag tror att Henrik har en enklare lösning.

Jag är rätt övertygad om att mattekalles metod är optimal: i varje kast ger ett av utfallen ett avslut, och vi kommer aldrig hitta en metod som garanterat är slut på ett ändligt antal kast eftersom 2^n inte är delbart med 3 för något n.

Generell metod, för att ge utfall A sannolikhet p och utfall B sannolikhet q=1-p:

Låt "kvarvarande sannolikhet" efter n kast vara pn resp qn för de två utfallen, p0=p, q0=q.

För varje kast n, välj utfallet med högst kvarvarande sannolikhet om du får klave i varje kast t.o.m n-1 och krona i kast n, och subtrahera motsvarande kvarvarande sannolikhet med (1/2)^n.

I fallet med sannolikheten för A = 1/3:

kr: B (kvarvarande sannolikhet p1=2/3-1/2=1/6

kl-kr: A (kvarvarande q2=1/3-1/4=1/12)

kl-kl-kr B (p3=1/6-1/8=1/24)

I fallet med p=pi-3 blir följden

BBABBABBBBAAAAAA... (sannolikheten att ingen krona kommit på 16 kast är 8*10^-6)

När man singlar bygger man bit för bit upp ett binärt tal mellan noll och ett. Så snart man ser att detta tal är mindre än p eller att det är större än p avbryter man. Om p är en tredjedel, alltså binärt p=0.01010101... blir det likvärdigt med mattekalles algoritm. Förvätat antal kast är två om p har oändlig binär utveckling. (Bevisa det utan räkningar!) Om p är av typen n/2^k blir förväntat antal kast lägre eftersom det aldrig behövs fler än k kast. Med p=1/2 tar det förstås alltid ett kast och med p=0 eller p=1 tar det noll kast.

Väntevärdet är ju 2 så att i de flesta fall kommer man till ett avslut ganska snabbt. Sedan har vi de fall där man får som sagt singla slanten många gånger. Men de uppvägs av att man ofta får ett avslut redan efter ett kast. Så jag anser att metoden är ganska effektiv. Vi får se vad Henrik har för kommentar. 

Ett förtydligande på haraldfreijs kombination BBABBABBBBAAAAAA...

Konverterar vi $\mathrm{\pi }-3$ till binärt så får vi

$$\begin{gathered} 0.0010010000111111..{.}_2 där \\ BBABBABBBBAAAAAA... \end{gathered}$$ 

Vi ser att efter decimalkommat har vi alltså haraldfreijs kombination.

Kort bevis för att väntevärdet är två: x=0.5*1+0.5*x.
Ännu kortare bevis: 0.5 avgörande/kast => 2 kast/avgörande.

Nu är det mattekalles tur.

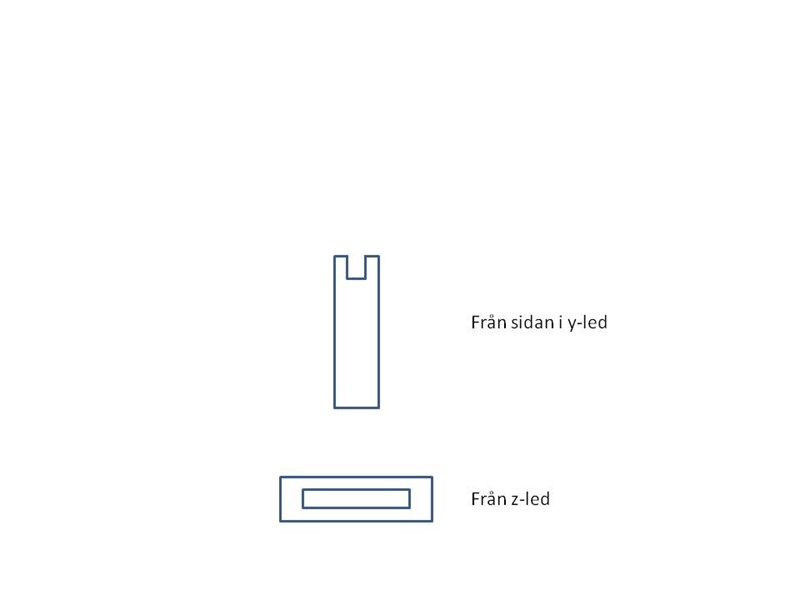
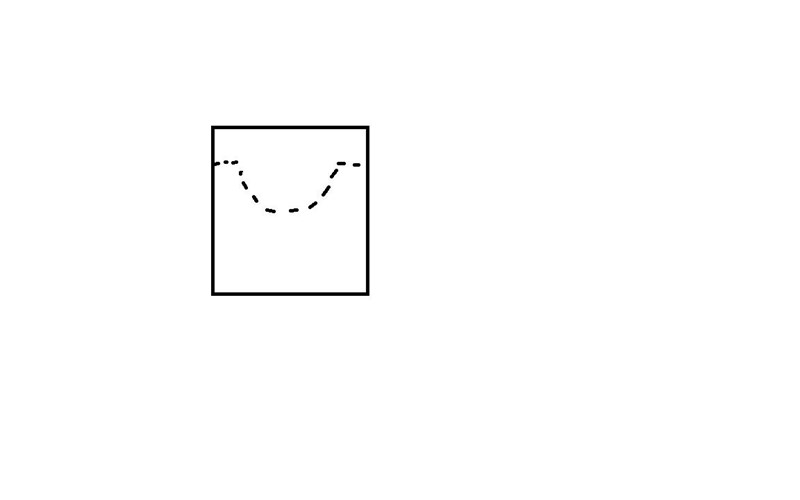
Här kommer nästa kluring.
En figur ser ut från två av tre vyer enligt beskrivningen ovan. Hur ser den ut i vyn som är i x-led.

Jag tror att den figur du föreslår skulle se ut så här från z-led. Det stämmer inte riktigt.

Du har rätt. Nytt försök:

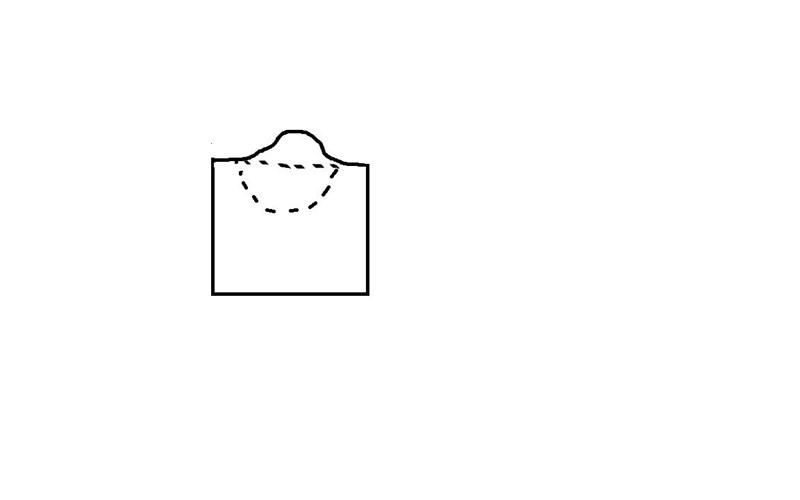
Jag tror att den figur du föreslår skulle se ut så här från z-led. Det stämmer inte riktigt men nu är det inte långt bort.

Nej, eftersom bågen uppåt börjar med en kurva kommer den inte synas i z-led. Lite bättre ritning (men ack så dålig)

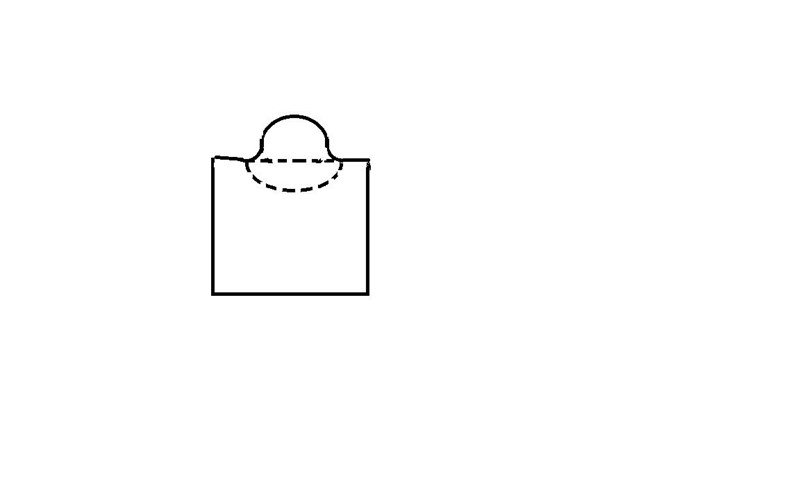
Jag tror att den figur du föreslår skulle se ut så här från y-led. Det stämmer inte riktigt men nu är
det inte långt bort, dvs tänk kurvor.

Här kommer ett rätt svar på kluringen: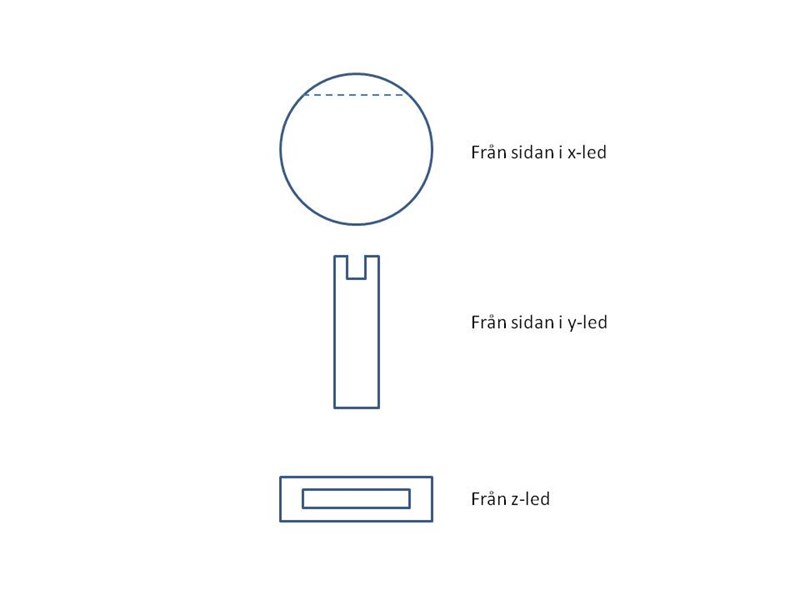Dags för nästa kluring:

I hörnet A i ett rum befinner sig en spindel som snarast möjligt vill ta en fluga i hörn B. Rummet är
4 Längdenheter (Le) brett, 4 Le högt och 8 Le långt. Spindeln kan röra sig dubbelt så snabbt på vägg som på golv.

Spindeln har tre vägar att välja på:

1. Den kortaste vägen r1 om han kombinerar vägg- och golv-spring.
2. Den snabbaste vägen r2 med kombination vägg- och golv-spring.
3. Den snabbaste och kortaste vägen r3 om han endast gör vägg-spring.

Vilken väg tar längst tid och hur mycket procentuellt snabbare är de övriga valen i tid.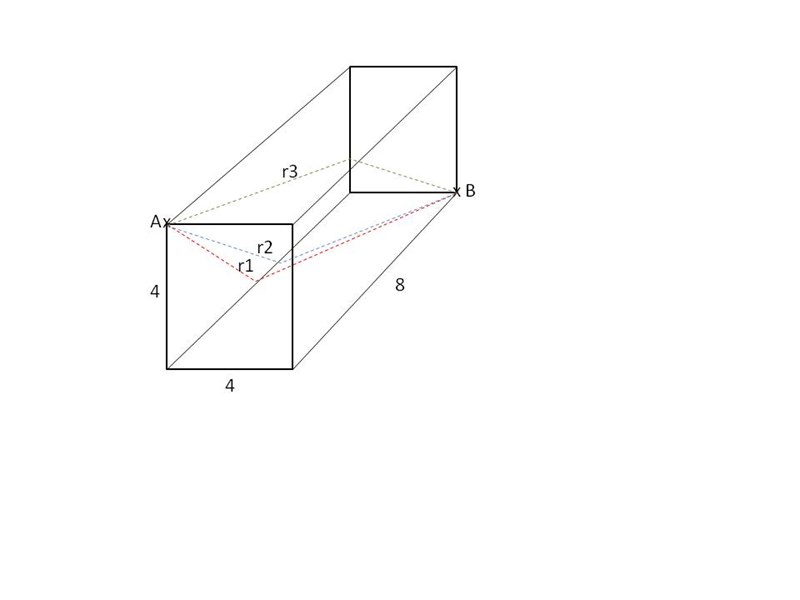

Med hastighet 1 på vägg och 1/2 på golv är tiden $t=s_{vägg}+2s_{vägg}$.

Kortaste vägen på väggen är en diagonal genom en rektangel med sidorna 4 och 12 (4+8) =>$t=s_{vägg}=\sqrt{4^2+{12}^2}=4\sqrt{10}\approx 12.65$

Kortaste vägen på golv och vägg är antingen en diagonal genom en rektangel med sidorna 8 och 8 (4+4), där hälften springs på golv och hälften på vägg => $t=\frac{3}{2}8\sqrt{2}=12\sqrt{2}\approx 16.97$, eller samma sträcka som ovan fast där 8/12 av sträckan springs på golv => $t=\frac{2\times 8+4}{12}4\sqrt{10}=\frac{20}{3}\sqrt{10}$, vilket är längre.

Snabbaste sträckan över golv och vägg måste också passera en lång kant (kortare sträcka och större andel över vägg). Benämn avståndet från hitre väggen till kantpassagen x. Då är

$$\begin{gathered} t=2\sqrt{x^2+4^2}+\sqrt{(8-x{)}^2+4^2} \\ t\text{'}=\frac{2x}{\sqrt{x^2+4^2}}-\frac{8-x}{\sqrt{(8-x{)}^2+4^2}} \end{gathered}$$

t'=0 ger 

$$\begin{gathered} x\approx 1.847 \\ t\approx 16.151 \end{gathered}$$

(okej, jag löste numeriskt, finns det något snyggt sätt att lösa fjärdegradaren analytiskt?).

Snabbast är alltså att bara springa på vägg. Att springa raka vägen på golv och vägg tar 34 % längre tid och att springa snabbaste vägen på golv och vägg tar 28% längre tid.

Rätt svar! Notera bara att den första
$t= s_{vägg}+2s_{vägg}$

gäller bara om
$s_{golv}=s_{vägg}$

Bra jobbat haraldfrej. Nu är det din tur

Haha, jo, så kan man se det :).

På en tavla står talet ${10}^{2017}$ skrivet. Två spelare turas om att göra ett av två tillåtna drag:

• Ersätta ett tal x på tavlan med två tal a & b, sådana att x = ab
• Stryka ett av två identiska tal på tavlan.

Man förlorar om det inte finns något tillåtet drag när det är ens tur. Vilken av spelarna vinner (om hen spelar optimalt)?

EDIT - Det var ju helt feltänkt...gut feeling failure.

Totalt antal drag är 2016 + 2016 + 2016 + 2016 = 8064, dvs ett jämnt antal drag 

Alltså vinner den spelare som inte börjar.

Ser inte hur du räknar antalet drag? Beroende på dragföljd kan det variera. De två dragföljderna 

2^2017->2;2^2016->2;2;2^2015->2;2^2015->2;2;2^2014->2;2^2014->2;2;2^2013->2;2^2013

2^2017->4;2^2015->4;4;2^2013->4;2^2013->2;2;2^2013->2;2^2013

har samma t.ex. start och slutpunkt, men olika antal drag däremellan

Ja jag tänkte att man först skulle faktorisera och sedan reducera. Men det blev ju helt fel.

Antar att a,b>1 annars är det ingen som förlorar.

När A står i tur finns alltid udda antal tal, enda slutställningen är {2,5} så B förlorar.

Ja, det var ju en betydligt enklare lösning än den jag tänkte. Helt rätt, Henrik, din tur.

Ett liknande spel då. A får talet 2017, delar det i två termer, båda positiva heltal, till exempel 1000+1017 och lämnar över det till B som nu får välja första eller sista termen, dela upp den i två termer och sätta den ena först, den andra sist och lämna över till A, till exempel 999+1017+1 eller 2+1000+1015. Den som inte kan följa reglerna förlorar. (Tips: man förlorar om uttrycket är 1+...+1.) Vem vinner?

En position är alltså en heltalssumma och ett drag är att ta första eller sista termen, dela den i två och sätta den ena först och den andra sist.

B vinner.

Ett tal som inte står först eller sist kan aldrig påverka vad som står först eller sist senare, eftersom man bara "bygger på" utifrån. Det enda som är intressant i en position är alltså första och sista talet (och deras respektive position är också ointressant).

Om man lämnar ifrån sig två udda tal kommer man att få tillbaka ett udda och ett jämt, eftersom nästa "ytterpar" kommer vara en termuppdelning av ett av de två udda talen. Man har då möjlighet att dela upp det jämna talet i två udda. Har man en gång lämnat ifrån sig två udda tal kan man alltså göra det resten av spelet. Eftersom den enda vinnande positionen är 1,1, som är ett udda par, det finns ett ändligt antal positioner, och man aldrig kan återvända till en tidigare position (eftersom summan av de två talen är ett av talen i föregående position), vinner den första som kan lämna ifrån sig ett udda par. A måste dela upp 2017 i ett udda och ett jämt tal, och B kan dela det jämna i två udda och därifrån vinna.

Utmärkt svar! Och eftersom jag hittade på problemet själv kan du inte ha googlat fram det.

På en skola med årskurs 1-5 får eleverna följande problem: Välj ut två personer från varje årskull, och ställ dem på en rad, så att det står en person mellan de två ettorna, två personer mellan de två tvåorna, tre personer mellan treorna osv.

Lyckas eleverna, och i så fall hur?

Behövs det en ledtråd här?

Det är kanske dags att plocka fram en gammal kortlek och försöka arrangera 10 kort på det sättet du önskade.

Skrev du rätt i uppgiften? "...och ställ dem på en rad, så att..."

Om varannan ruta i raden är svart och varannan vit, så kommer tvåorna att finns på olikfärgade rutor, likaså fyrorna. Kvar finns tre vita och tre svarta rutor och eftersom ettorna finns på två likfärgade rutor, likaså treor och femmor, så är det omöjligt. Samma resonemang visar att det bara kan funka om 5 byts mot något av 3, 7, 11, ...

Helt rätt

Markerar man positionerna där eleverna ska stå med siffrorna 1-10 så inser man att antalet elever på en jämnsiffrad position måste vara 2,4,6 eller 8, alltså 4 jämnsiffrade positioner. Men antalet jämnsiffrade positioner är 5. Det är alltså omöjligt.

Henrik hade alltså redan lämnat rätt svar, och han har därmed bollen.

a. Hur stor del av en kon kan ett klot uppta? Klotet ska alltså finnas helt inne i konen.

b. Samma fråga med glasstrut och glasskula, som ju får sticka upp ur struten,

a)

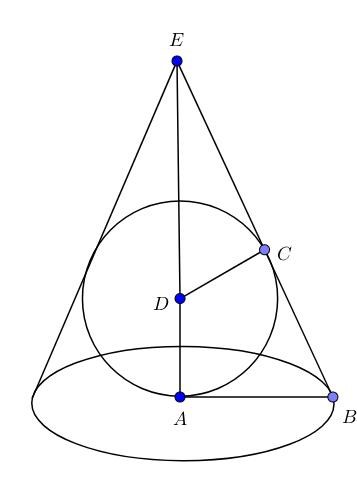
Enligt figuren så är $∆ABE~∆CDE$. Väljer man radien sådan att $\measuredangle CDE=\mathrm{\pi }/2=\measuredangle ABE$, och för aritmetisk enkelhet betecknar $AE=h$, $CD=r$ och $AB=k$ så får man av Pythagoras sats att

     $BE=\sqrt{A{E}^2+A{B}^2}=\sqrt{h^2+k^2}.$

likformighet att

     $\frac{AB}{BE}=\frac{CD}{DE}\iff \frac{k}{\sqrt{h^2+k^2}}=\frac{r}{h-r}\iff r=\frac{hk}{\sqrt{h^2+k^2}+k}.$

Beräknar man volymerna av de geometriska kropparna får man att

     $\begin{array}{rcl}{V}_{klot}& =& \frac{4\mathrm{\pi }{\left({\displaystyle \frac{hk}{\sqrt{h^2+k^2}+k}}\right)}^3}{3}=\frac{4\mathrm{\pi }{h}^3{k}^3}{{\displaystyle 3{\left(\sqrt{h^2+k^2}+k\right)}^3}}\\ V_{kon}& =& \frac{\mathrm{\pi }h{k}^2}{3}\end{array}$

Förhållandet blir

     $f\left(h,k\right)=\frac{V_{klot}}{V_{kon}}=\frac{4h^{2}k}{{\left(\sqrt{h^2+k^2}+k\right)}^3}.$

Vidare så gäller det att $f\text{'}(h,k)=4k\left(h^3+2h{k}^2\right)/{\left(h^2+k^2\right)}^{5/2}$ och att

     $\max \left\{f\left(h,k\right)\right\}=\frac{1}{2}=50\%.$

_____________________________________________________________________________

b) Denna var lite jobbigare. Min första tanke var att den volym inuti en strut som en kula kan anta när den läggs på en strut är maximal då kulans radie är lika med konens botten radie. Men vid närmare eftertanke så är inte detta villkor alltid gällande. 

Så långt är det rätt! Nu över till glasstruten.

Henrik Eriksson skrev :

Så långt är det rätt! Nu över till glasstruten.

Yes, håller på och tänker så det ryker. Den såg så enkel ut när jag snabbt läste igenom den. Men ack så fel jag hade. 

Eftersom a-frågan är  "Hur stor del av en kon kan ett klot uppta?" så måste
svaret gälla för alla former av en kon, dvs även en kon vars höjd = 4 x klotets radie.

Med beteckningar enligt Lirim.K's fina figur ovan:
Klotets radie =  DA = DC = 1
Konens höjd = AE = 4
DE = 3
CE = $\sqrt{3^2 - 1^2 }$ =  $\sqrt{8}$
AB = $\frac{4 \times 1}{\sqrt{8}}$ = $\sqrt{2}$

Klotets volym = $\frac{4 \times 1^{3 } \times \mathrm{\pi }}{3}$ = $\frac{4}{3} \times \mathrm{\pi }$

Konens volym = $\frac{4 \times {\sqrt{2}}^2 \times \mathrm{\pi }}{3}$ = $\frac{8}{3} \times \mathrm{\pi }$

Klotets volym  =  $\frac{1}{2}$ $\times$ Konens volym

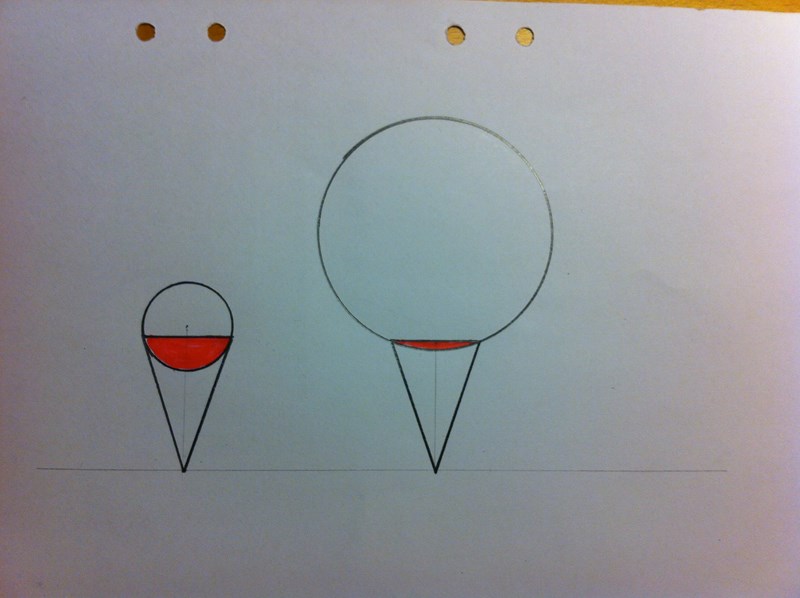
B-frågan har inget svar  "Samma fråga med glasstrut och glasskula, som ju får sticka upp ur struten".

Bilden nedan visar två identiska glasstrutar, men som har olika stora glasskulor.
Den röda delen av glasskulan är nere i struten, resten sticker upp ur struten.
Så om frågan är "Hur stor del av en kon kan ett klot, som får sticka upp ur konen, uppta?", då
finns inget svar.

Om man tolkar frågan som "Hur stor del av en kon kan ett klot (som får sticka upp ur konen) som mest uppta?" så finns det ett svar.

Jag tolkar det som ett optimeringsproblem, precis som Yngve har skrivit. Men jag blir fundersam, svaret är väl olika beroende vilka dimensioner konen har och dess toppvinkel? 

Hm, varför skulle frågan gälla en viss kon? Det gäller maximering över alla strutar och alla glasskulor.

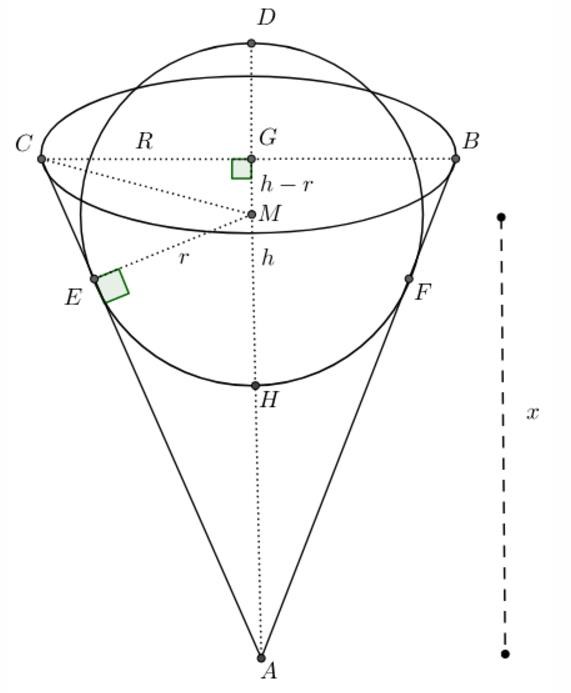
Skulle denna bilden sätta mig på rätt spår? Variablerna är för många, jag får en funktion av fyra variabler för förhållandet och klarar inte riktigt av att uttrycka alla variabler i en annan. Uttrycken blir skrämmande "nested radicals" och jobbiga att arbeta med.

Behöver man använda någon integrationsteknik eller går det att lösa geometriskt med envariabelanalys och derivata?

Envariabelderivering duger bra.

Med "alla strutar" menar du då att även konens toppvinkel får variera mellan 0 och 180 grader? För om klotets radie, konens vinkel, konens radie, konens höjd får variera så finns det inget max eftersom man kan skala upp dimensionerna eller skala ner dem hur man vill och ändå få samma förhållande mellan volymerna. Det måste finnas mer information om vad som är konstant och inte konstant.

Du kan ju tex sätta klotets radie konstant och sedan variera på konens vinkel och konens höjd för att se var max finns. Konens radie finns ju implicit om du vet konens vinkel och konens höjd.

mattekalle skrev :

Du kan ju tex sätta klotets radie konstant och sedan variera på konens vinkel och konens höjd för att se var max finns. Konens radie finns ju implicit om du vet konens vinkel och konens höjd.

Varför gör du inte det? Detta är ju en öppen tråd som alla kan deltaga i, inte bara jag. 

Men för att spinna vidare på ditt inlägg, han skriver ju att det ska kunna gälla för vilken sfär som helst. Alltså kan ju inte klotets radie vara konstant, den måste tillåtas variera med.

Jag förstår inte vad förvirringen gäller. Det första uppgiften med ett klot inne i en kon hade inte heller någon begränsning. Maximeringen gällde över alla koner och alla klot och så är det i strutfallet också.

Förvirringen är att det i b) inte riktigt går att uttrycka konens botten radie i termer av klotets radie. Eller går kanske det gör men jag har inte hittat den vägen. Ännu.

Din fina figur har h, r och vinkeln v. Eftersom bara proportionerna är intressanta kan man ju sätta r=1 så det blir bara två variabler kvar.

Låt $\measuredangle EAM=v$. Från figuren får man att konens radie är

     $R=h\tan \left(v\right)\Rightarrow AC=\sqrt{{\left(h\tan \left(v\right)\right)}^2+h^2}=h\sqrt{1+{\tan }^2\left(v\right)}.$

Likformighet mellan $\measuredangle ACG$ och $\measuredangle AEM$ ger

     $\frac{1}{AM}=\frac{R}{AC}\iff \frac{1}{AM}=\frac{h\sqrt{1+{\tan }^2\left(v\right)}}{\sqrt{{\displaystyle h}{\displaystyle 2}\left(1+{\tan }^2\left(v\right)\right)+h^2}}=\frac{\sqrt{1+{\tan }^2\left(v\right)}}{\sqrt{2+{\tan }^2\left(v\right)}}.$

Detta ger att

     $$\begin{gathered} AM=\frac{\sqrt{2+{\tan }^2\left(v\right)}}{\sqrt{1+{\tan }^2\left(v\right)}}=\sqrt{\frac{2+{\tan }^2\left(v\right)}{1+{\tan }^2\left(v\right)}}=\sqrt{\frac{1}{{\displaystyle 1}{\displaystyle +}\cos {\displaystyle {}^2}{\displaystyle (}{\displaystyle v}{\displaystyle )}}} \\ GM=h-AM=h-\sqrt{\frac{1}{{\displaystyle 1+{\cos }^2\left(v\right)}}}. \end{gathered}$$.

Använder man formel (6) här, så gäller det att volymen för den del av sfären som är innuti konen (och konen) är

     $$\begin{gathered} V_{cap}=\frac{\mathrm{\pi }·G{M}^2\left(3-GM\right)}{3}=\frac{\mathrm{\pi }·{\left(h-\sqrt{\frac{1}{{\displaystyle 1+{\cos }^2\left(v\right)}}}\right)}^2\left(3-\left(h-\sqrt{\frac{1}{{\displaystyle 1+{\cos }^2\left(v\right)}}}\right)\right)}{3}. \\ {V}_{kon}=\frac{\mathrm{\pi }h{R}^2}{2}=\frac{\mathrm{\pi }{h}^3\left(1+\tan \left(v\right)\right)}{2}. \end{gathered}$$

Förhållandet blir

     $f\left(h,v\right)=\frac{V_{cap}}{V_{kon}}=\frac{\frac{\mathrm{\pi }·{\left(h-\sqrt{\frac{1}{{\displaystyle 1+{\cos }^2\left(v\right)}}}\right)}^2\left(3-\left(h-\sqrt{\frac{1}{{\displaystyle 1+{\cos }^2\left(v\right)}}}\right)\right)}{3}}{{\displaystyle \frac{\mathrm{\pi }h\left(1+\tan \left(v\right)\right)}{2}}}.$

Denna är inte rolig att arbeta med. Jag tror att jag gör det krångligare än vad det är. Ska titta på det lite närmare under kvällen.

PS. Börjar bli dags med en ny tråd. Får felmedelande och kan inte längre redigera mitt inlägg här.

Låt v vara konstant och sök h först!

Innan jag börjar kladda till med en lösning, är svaret 8/9? Alltså typ 89%?

Nytt försök:

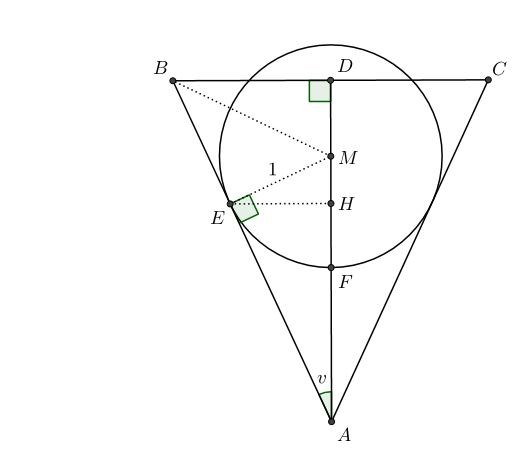
Jag betecknar $\angle EAM=v$ och låter denna vinkel vara konstant. Det gäller då av grundläggande trigonometri att $AE=1/\tan \left(v\right)=\cos \left(v\right)/\sin \left(v\right)$ och $AH=AE·\cos \left(v\right)=\left(\cos \left(v\right)\sin \left(v\right)\right)·\cos \left(v\right)={\cos }^2\left(v\right)/\sin \left(v\right).$ Sätter man $DH=x$ så är konens totala höjd lika med

     $AD=AH+DH=\frac{{\cos }^2\left(v\right)}{\sin \left(v\right)}+x.$

Längden från sfärens botten till $F$ till konens cirkulära plan i punkten $D$ är lika med $DF=1-\sin \left(v\right)+x.$ Detta fås genom att notera att för $\angle EHM$ så gäller det att $MH=ME·\sin (\angle MEH)=1·\sin \left(v\right)=\sin \left(v\right)$ eftersom $ME=1$ och p.g.a likformiga trianglar så är $\angle MEH=v$. Så

     $DF=DH+HF=DH+MF-MH=1-\sin \left(v\right)+x.$

Vi bildar nu funktionen

     $f\left(x\right)=\frac{\mathrm{\pi }D{F}^2\left(3-DF\right)/3}{\mathrm{\pi }A{D}^3·{\tan }^2\left(v\right)/3}=\frac{{\left(1-\sin \left(v\right)+x\right)}^2\left(2+\sin \left(v\right)-x\right)}{{\left({\displaystyle \frac{{\cos }^2\left(v\right)}{\sin \left(v\right)}}+x\right)}^3·{\tan }^2\left(v\right)}.$

Denna funktion antar maximum då $x=1-\sin \left(v\right).$ Beräkning av $f(1-\sin (v\left)\right)$ ger en ny funktion i termer av $v$

     $f_{\max }\left(x\right)=f\left(v\right)=\frac{4{\left(1-\sin \left(v\right)\right)}^2\left(1+2\sin \left(v\right)\right)}{{\left(1-\sin \left(v\right)+{\displaystyle \frac{{\cos }^2\left(v\right)}{\sin \left(v\right)}}\right)}^3·{\tan }^2\left(v\right)}.$

Denna funktionen antar ett maximalt värde $8/9$ för $v=\mathrm{\pi }/2.$ Dock så kommer aldrig vinkeln kunna bli $\mathrm{\pi }/2$eftersom konen då blir en 2D cirkel. Analogt gäller det att om $v\to 0$ så blir konen en rät linje. Alltså gäller det att $0<v<\mathrm{\pi }/2.$ Man får slutligen att

     $f_{\max }=\underset{v\to \mathrm{\pi }/2}{\lim }f\left(v\right)=\frac{8}{9}\approx 89\%.$

Utmärkt! Av konens volym kan alltså högst hälften fyllas av ett klot men av strutens volym kan en glasskula fylla hur nära 8/9 som helst. Jag bara uppfann ett problem som skulle vara lagom svårt men hade inte vågat hoppas på ett så snyggt svar.

Hur ser lösningen ut om man sätter siffror (ett exempel) på:
Vinkeln vid A
Avståndet AD
Avståndet AM
Radien på kulan

@Henrik: Ja det var ganska svår. Höll på med den väldigt många timmar på arbetstid, så detta var nog den mest icke produktiva veckan någonsin för mig på jobbet.

@Larsolof: Jag misstänker att om man bara använder fasta värden så får man ett svar som är under 8/9 (om man mot förmodan inte råkar använda väldigt perfekta värden). Man måste använda gränsvärde för att nå rätt svar.

---Jag skapar en ny tråd för denna har blivit för lång. Jag slänger även in nytt problem i den andra tråden. Moderator kan låsa denna om hen vill.---

Tråden låst på begäran, nya kluringar hittas i denna tråd.