ODE med Fourier transform

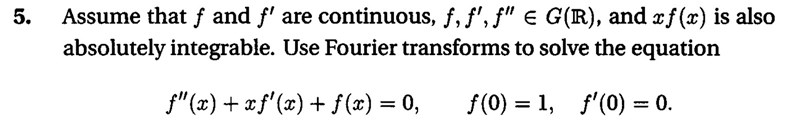
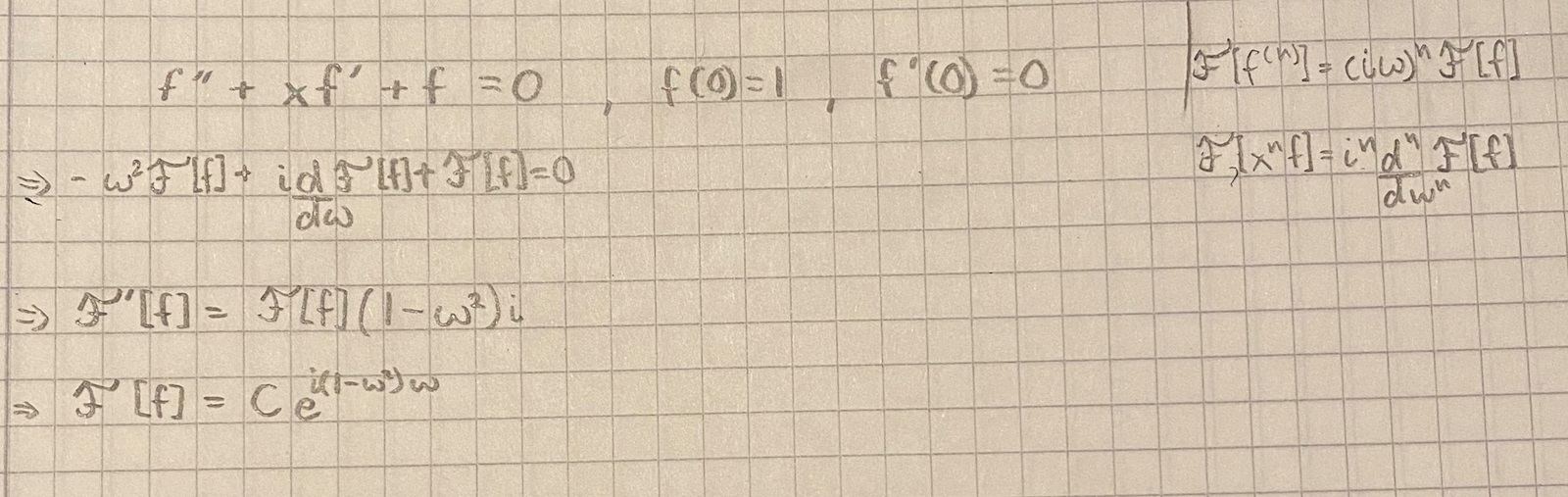
Jag är inte helt med på vad du gör, men tänk på att $xf^\prime(x)+f(x)=(xf(x))^\prime$ och om jag inte ser fel har du transformationer som kan fixa det åt dig upp till höger. Ta bara ett steg i taget och håll ordning på vad som är funktionen.

Mer hjälp

Tack så jättemycket! Jag vet inte riktigt hur jag fick det så pass fel först, men insåg sen precis som du sa att det blev en mycket enklare diff-ekvation. Jag får att F=ce^(-w^2/2). Finns det något enklare sätt att beräkna inversen för att få fram f, eller måste jag beräkna den här integralen?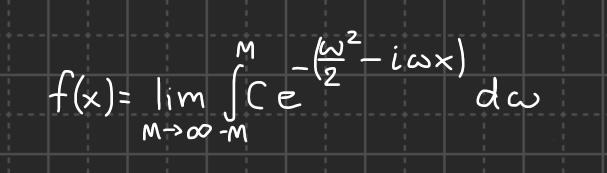 

Det enklaste är att använda en formelsamling, t.ex. Beta, eller läroboken där härledningen förmodligen dyker upp tidigt. 

$\mathfrak{F}[e^{-ax^2/2}]=\sqrt{\frac{2\pi}{a}}e^{-\omega^2/2a}$

Jag tror det är tänkt att ni ska använda den, åtminstone om det är första gången ni stöter på det här och ännu inte lärt er den inversa transformationen. $a=1$ i ditt fall.

Vill du härleda den själv för hand bör du känna till standardintegralen

$\displaystyle \int_{-\infty}^{\infty}e^{-y^2}dy=2\int_{0}^{\infty}e^{-y^2}dy=\sqrt{\pi}$

Hur du går till väga beror på vilken årskurs och vad du känner till sedan tidigare. Min favorit är att