Öka cirkelns area med 50%
Hej!
jag hade behövt lite hjälp med att komma på en bra metod för att lösa följande uppgift:
 en tanke jag hade var att skriv upp formeln för den nya arean och dividera det på formeln för den gamla arean och att det Ska vara lika med 1,5 men eftersom att man inte vet vad radien är från början eller något så har jag svårt att hitta ett bra sätt att lösa uppgiften.
en tanke jag hade var att skriv upp formeln för den nya arean och dividera det på formeln för den gamla arean och att det Ska vara lika med 1,5 men eftersom att man inte vet vad radien är från början eller något så har jag svårt att hitta ett bra sätt att lösa uppgiften.
här är ett FÖRSÖK (med betoning på försök) till en lösning, men insåg när jag kom till slutet att det inte skulle funka:

tacksam för all hjälp☺️
Snabb fråga: Kommer du ihåg längdskala, areaskala, volymskala från högstadiet? I det här fallet är det faktiskt riktigt användbart.
Återkommer när jag kikat på din uträkning.
Tror att jag minns det. Det var la att areaskalan är längskalan2 och volymskalan var längskalan3?
ska man skriva ett förhållande mellan längskalan samt ett förhållande för areaskalan där svaret ska vara 1,5?
Det stämmer.
Du vet att A' (nya arean) skall vara 1,5A. Areaskalan är alltså 1,5. Då blir längdskalan , alltså en ökning med 22%.
Kikar jag på din uppställning så ser jag ett fel direkt:
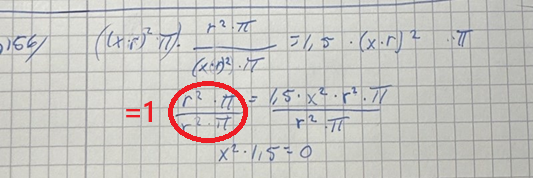
Jag fortsätter din beräkning:
Eftersom du ställde den lilla cirkeln i täljaren och den större i nämnaren så har du fått förändringsfaktorn om arean skall minska med 50%.
Det är lättfixat:
Så här hade jag kanske ställt upp det:
Ja, det stora cirkeln borde varit i täljaren. Men hur kunde man bara ”fixa” det så lätt genom att dividera 1 med förändringsfaktorn för om det hade minskat med 50%?
din metod var betydligt enklare!
En kvadrats area förändras från 4 ae till 9 ae:
Det är en förändring med (2,25-1)= 125%, alltså en ökning.
En kvadrats area förändras från 9 ae till 4 ae:
Det är en förändring med ca (1-0,44)=56%, alltså en minskning.
Vad du jämför med vad är alltså bara frågan om vad du sätter i täljare/nämnare.
oki, tack för hjälpen och tydliga förklaringar :D


