Oklart i boken
Jag vet att jag har lovat att inte spamma men detta är verkligen oklart för mig. Jag kan inte förstå en annat förklaring jag fick från pi-streck eftersom detta har jag inte assimilerat...
Vad har linjär självständighet att göra med noll koefficienter?


Du kan inte kombinera ihop v och w så att Av+Bw får samma riktning som u.
Om Cu+Av+Bw har längden noll i u:s riktning, så måste det bero på att C är noll.
Tack, det blev liiite klarare.
Är det allt som sägs i den här stycke? Jag ska försöka förklara det för mig själv, säg till om det stämmer!
1. Eftersom vektorer är linjärt oberoende (de tensar rummet i olika håll), de blir noll vektor bara om deras koefficienter är noll.
Det ser ut såhär:
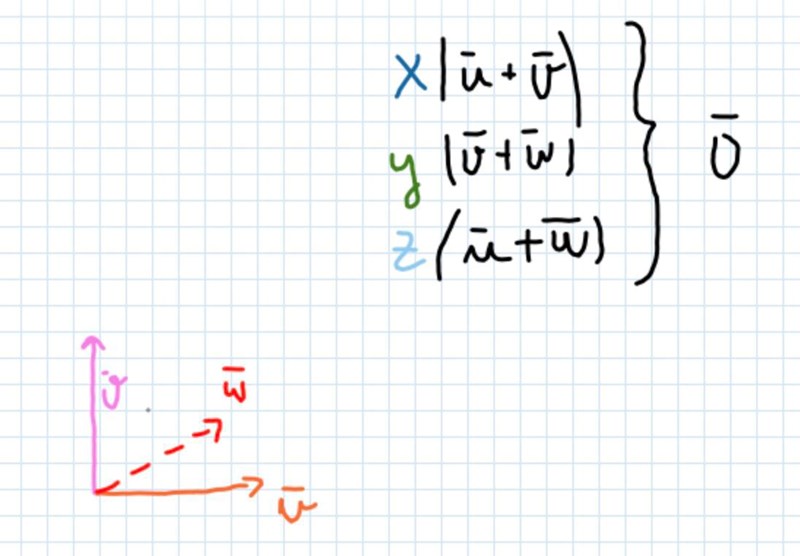
2. Det läggs på variabel framför varje par vektor som adderas .
3. I steg 3 varje variabel multipliceras in i parentes och omflyttas så att vi har en parentes av variabel istället framför ursprungliga vektorer.
4. Nu kan vi konstatera att $$(\overline{u},\overline{v}, \overline{w}) pekar fortfarande åt olika hål, så den enda sätt att få noll vektorn är att alla kombinationer av variabler blir noll.


