Gällande olika konventioner av Fouriertransformer/Parsevals formel

Hej,

jag har svårt för uppgifter om Fouriertransformer, inverser och Parsevals formel osv. Har stött på massa olika formler, och vet inte riktigt vilka jag ska hålla mig till. Min lärare använder dessa kombinationer:

Men vilken formel för Parseval ska jag då använda? Jag fastnade speciellt i denna uppgift:

Jag har lyckat lösa första delen av frågan genom att använda formeln för Fouriertransoformen som min lärare använder, och fick då att 𝐹 [𝑓] (𝜔) = $\frac{\sin (w b)}{w π}$ . Men jag vet inte hur jag ska gå vidare med den andra delen av frågan.

Min lösning:

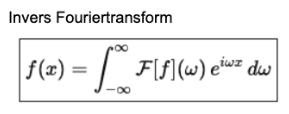
Jag är också lite osäker vad de söker efter (had dock inte hållit på särskilt mycket med fouriertransformer). En idé är att ifrån invers fouriertransformen får du att

$\displaystyle \pi f_b\left(x\right) = \int_{-\infty}^{\infty}\frac{\sin(b\omega)\cos(x\omega)}{\omega}d\omega$

där vi ignorerar imaginärdelen av $e^{i\omega x}$ eftersom den måste bli 0 (imaginär-integralen är även udda). En lösning som får fram rätt värde på integralen är att integrera båda led från 0 till $b$ map $x$ . I högerledet behöver man byta integrationordning och då även motivera att det är giltigt.

Jag tror en mer relevant funktion är samma som f_b, men den antar värdet $x$ när istället för 1. Det borde kringgå den extra saken med att integrera båda led. Har dock inte testat (har inget papper just nu!). (Har testat nu, det fungerar utan problem)

PS: Det finns även ett snabbare sätt att lösa integralen utan funktionen $f_b$ , genom att notera att

$\displaystyle \int_{-\infty}^\infty \frac{\sin^2(bx)}{x^2}dx=2 \int_{0}^\infty \frac{\sin^2(bx)}{x^2}dx$

(jämnt integrand). En partiell integration senare ger att det är en multipel av den ”kända” integralen sin(x)/x från 0 till $\infty$ .

Parsevals formler gäller sambandet mellan koefficienterna i Fourierserier och integralen av den periodiska funktionens kvadrat.

Här arbetar du med fouriertransformen av en icke-periodisk signal som definieras på hela reella talaxeln. Då är det Plancherels formler som ger motsvarande samband mellan integralerna av funktionen i kvadrat och av dess fouriertransform i kvadrat.

Med konventionen som du nämnt i ditt inlägg, så lyder Plancherels formel så här:

$\displaystyle \int_{-\infty}^\infty \left|f\left(x\right)\right|^2\,dx = 2\pi \int_{-\infty}^\infty \left|\mathcal{F}\left[f\right]\left(\omega\right)\right|^2\,d\omega$

När du sätter in $f_b$ och dess fouriertransform i denna formel, så får du

$\displaystyle \int_{-b}^b \left|1\right|^2\,dx = 2\pi \int_{-\infty}^\infty \left|\dfrac{\sin(\omega\,b)}{\omega\,\pi}\right|^2\,d\omega$ ,

så

$\displaystyle 2b = \frac{2}{\pi} \int_{-\infty}^\infty \dfrac{\sin^2(\omega\,b)}{\omega^2}\,d\omega$

Svara