Olika metoder att lösa en ekvation som saknar lösningar?

Min lsn:

Löste med determinantmetod och fick t=0 och -1, betyder det att det saknar lösningar då t är 0 eller -1? Och försökte först lösa frågan med gauss men kom ingen vart. Hur löser man a) med gauss?
Att du hittat rötterna t = 0 och t = -1 betyder att systemet antingen saknar lösningar eller har oändligt antal lösningar då t = 0 eller 1. Du kan hitta vilket det är genom att sätta in värdena och lösa systemet. :)
Att lösa det där med gauss direkt är säkert möjligt, om än tidskrävande, men varför?
pepparkvarn skrev:Att du hittat rötterna t = 0 och t = -1 betyder att systemet antingen saknar lösningar eller har oändligt antal lösningar då t = 0 eller 1. Du kan hitta vilket det är genom att sätta in värdena och lösa systemet. :)
Att lösa det där med gauss direkt är säkert möjligt, om än tidskrävande, men varför?
Ok försökte stoppa in t=0 i allafall och ser att den har oändliga lösningar då, men får inte fram parametriseringen!!
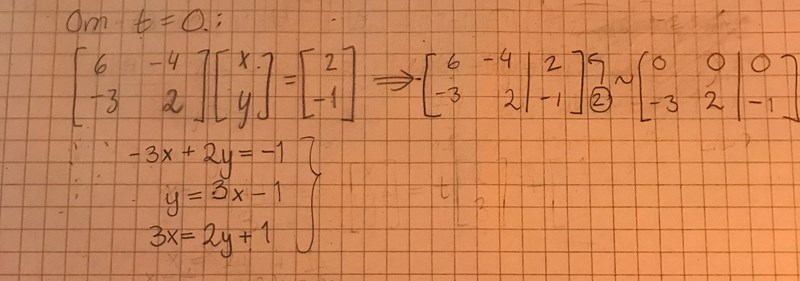
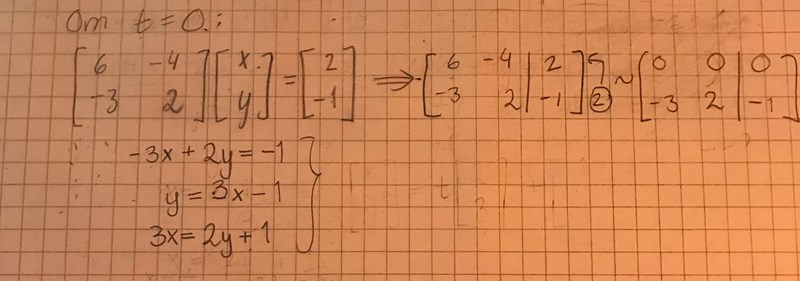
Du har ekvationen -3x + 2y = -1, mycket riktigt. Om du sätter y till t, får du att och y = t. Hur kan du skriva det som en punkt plus en vektor? :)
pepparkvarn skrev:Du har ekvationen -3x + 2y = -1, mycket riktigt. Om du sätter y till t, får du att och y = t. Hur kan du skriva det som en punkt plus en vektor? :)
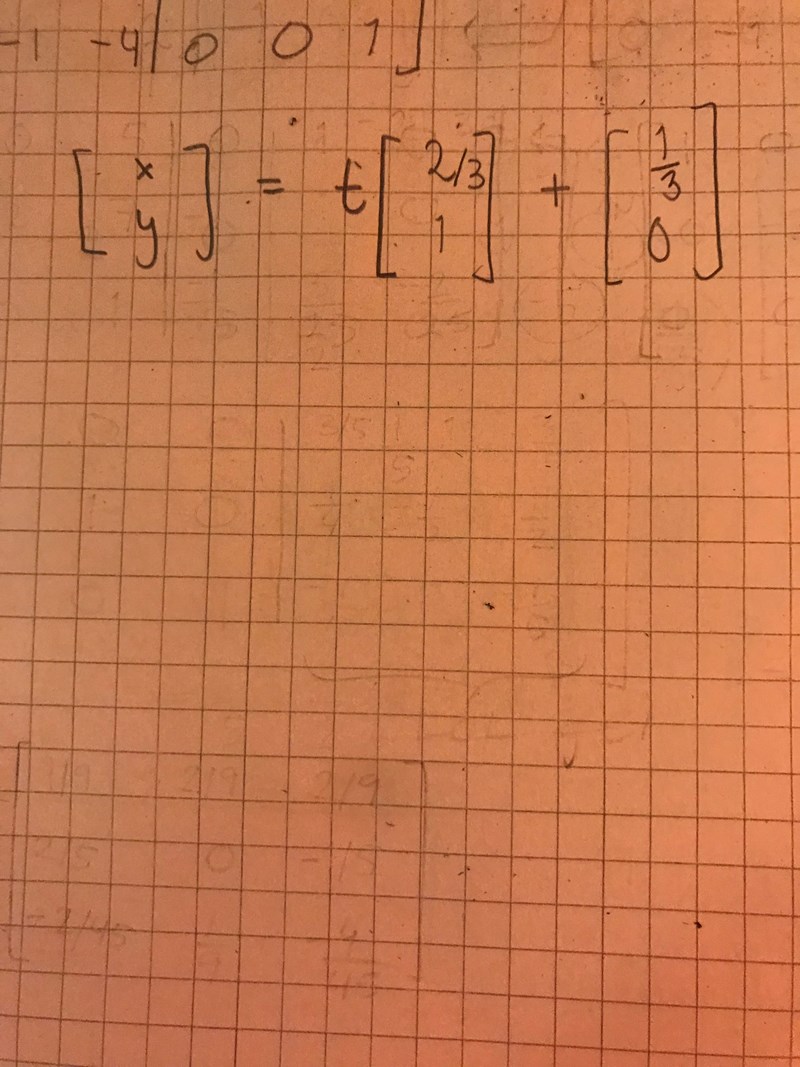
Jag får såhär, men i facit står det såhär:

De har förlängt vektorn med faktorn tre. Det går finfint att definiera y = 3t, och då få att x = 2t + 1, men det gör ingen skillnad för lösningsmängden. :) Med andra ord:


