Olika ”sin-värden”, hur gör man då?
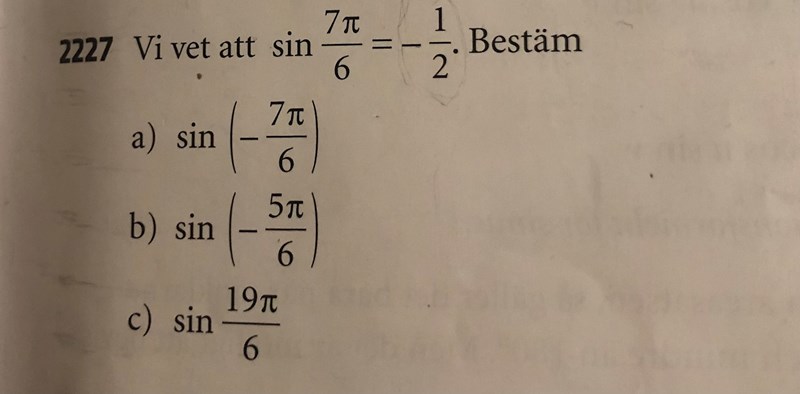 Hur gör man nu på b) när det är olika värden på sin?
Hur gör man nu på b) när det är olika värden på sin?
Sinus ar en periodisk funktion som varierar i steg av 0, 1, 0, -1, 0 for varje pi/2 radianer. Det ar val enklast att bara borja pa 0 radianer och rakna efter.
Hej!
Rita enhetscirkeln och markera vinklarna så löser det sig direkt. Man kan självklart lösa uppgiften utan, men det är som att använda derivatans definition för att derivera istället för deriveringsregler.
Förstår inte hur jag ska rita
offan123 skrev:Förstår inte hur jag ska rita
Vad är det du inte förstår hur du ska rita? Vet du vad enhetscirkeln är? Hur sinus värdet kopplas till enhetscirkeln? Vinklarna? Något annat?
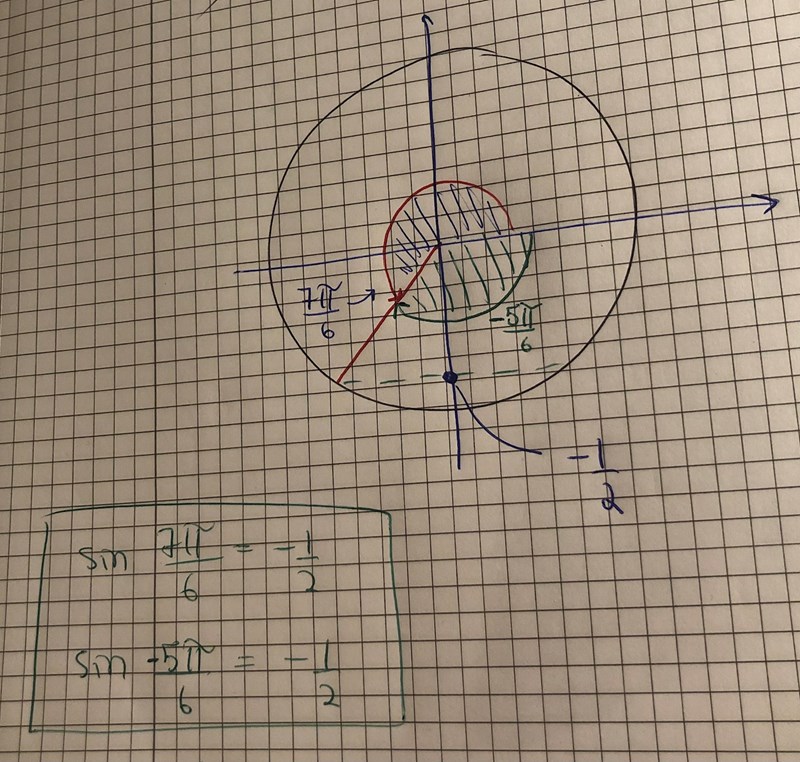 Men jag får inte bara fram positiv sin (7pi)/6 och inte negativ vinkel som i uppgiften. Vad gör jag för fel?
Men jag får inte bara fram positiv sin (7pi)/6 och inte negativ vinkel som i uppgiften. Vad gör jag för fel?
Men jag får inte bara fram positiv sin (7pi)/6 och inte negativ vinkel som i uppgiften. Vad gör jag för fel?
Du får ursäkta men jag förstår inte alls vad du försöker säga.
Men din bild är bra, du ser att och du vet ju värdet av .
Aha, då det blir bara -1/2.
Hur blir det på b)?
offan123 skrev:Aha, då det blir bara -1/2.
Hur blir det på b)?
Men det var ju b) vi gjorde. Menar du c)?
Menade c), skrev fel.
offan123 skrev:Menade c), skrev fel.
Då gör du på liknande sätt, men vinkeln bör ligga i intervallet . Vilken period har ?
2pi?
offan123 skrev:2pi?
Ja. Så för vilken vinkel (det finns flera val förstås, men jag tänker på om vi subtraherar lämpligt antal perioder) gäller att ?

