Olika svar beroende på metod, vid determinanträkning
Ordning
Tillåtna (nollskilda) produkter blir ju:
För att bestämma tecken för term 2 kollar jag på antalet inversioner, som är precis samma som antalet negativa par.
Produkt 2 kan skrivas såhär:
Vilket betyder att sviten av kolonnindex är följande:
n, 2, 3, ..., n-1, 1
2,3,...,n-1, 1 föregås av n => (n-1) inversioner
1 föregås av (n-1) => 1 inversion
Så totalt n inversioner => tecknet framför produkt 2) blir
Totalt blir det
Om man istället löser såhär:
Så frågan är nu, vad är det jag gör för fel i metod 1? Där beror tecknet på term 2, på om n är jämnt eller udda. Men det korrekta svaret fås ut genom metod 2. Skulle gärna vilja kunna lösa dessa genom de två olika metoderna (om det nu är möjligt?)
Bump
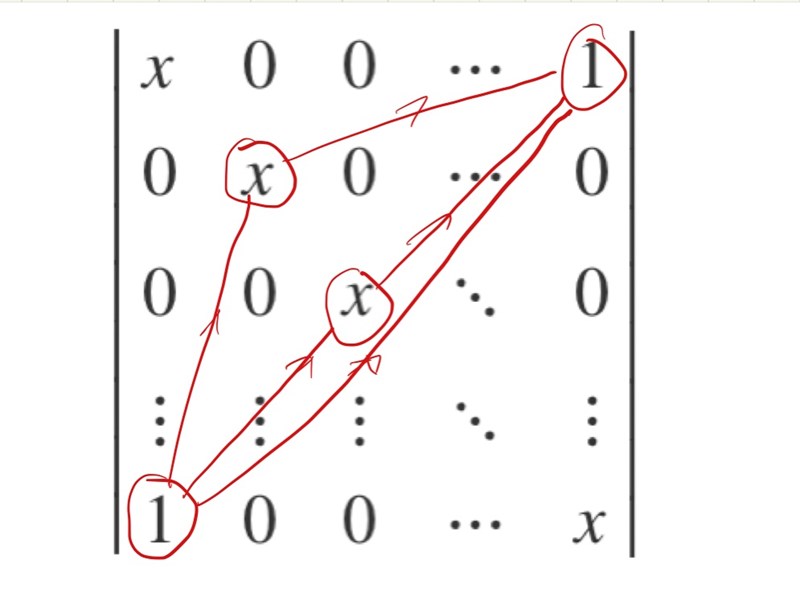
Antal inversioner = 2(n-2) + 1. (-1)2(n-2)+1 = -1.
Ja, juste! Missade att 1 föregås av 2, 3, ..., (n-1).
Då hänger jag helt med! Ytterst tacksam för svar!

