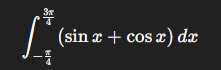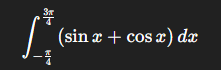Olika svar när jag integrerar med grader och radianer

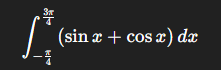
Dina trigonometriska deriverings- och integrationsregler bygger på att argumentet är i radianer. Annars behöver du skriva $\cos(x^{\circ})=\cos(\pi/180 \cdot x)$ som du kan använda dina vanliga regler på. 

MrPotatohead skrev:

Dina trigonometriska deriverings- och integrationsregler bygger på att argumentet är i radianer. Annars behöver du skriva $\cos(x^{\circ})=\cos(\pi/180 \cdot x)$ som du kan använda dina vanliga regler på. 

Beror detta på vilken miniräknare man använder då? Med papper och penna får jag samma svar oavsett grader eller radianer?

Pankakan skrev:
När jag gör den nedanstående beräkningen får jag 2.828 vilket stämmer för uppgiften, men om jag ställer om miniräknaren till att använda grader och sätter integrationsgränserna till 135 och -45 får jag istället 162?

Förhållandet är 57,3 eftersom 1 radian är 57,3^o.

Eftersom du också borde skala dx.

Pieter Kuiper skrev:

Pankakan skrev:
När jag gör den nedanstående beräkningen får jag 2.828 vilket stämmer för uppgiften, men om jag ställer om miniräknaren till att använda grader och sätter integrationsgränserna till 135 och -45 får jag istället 162?

Förhållandet är 57,3 eftersom 1 radian är 57,3^o.

Eftersom du också borde skala dx.

Hej! Jag dubbelcheckade, förhållandet mellan graderna jag använder och radianerna är 57,3 så verkar inte vara något problem där, men vad menas med att skala dx?

Pankakan skrev:

om jag ställer om miniräknaren till att använda grader och sätter integrationsgränserna till 135 och -45 får jag istället 162?

Då fick du 162^o som arean under grafen.

Pieter Kuiper skrev:

Pankakan skrev:

om jag ställer om miniräknaren till att använda grader och sätter integrationsgränserna till 135 och -45 får jag istället 162?

Då fick du 162^o som arean under grafen.

Intressant! Om Jag då delar 162 med 57,3 får jag rätt svar! Verkar då som att miniräknaren direkt kollar på arean mellan sin x och cos x istället för att göra beräkningar?

Miniräknaren gör som förväntat:
Det blir en yta som är 57 gånger större än om axeln hade varit i radianer.

Pieter Kuiper skrev:

Miniräknaren gör som förväntat:
Det blir en yta som är 57 gånger större än om axeln hade varit i radianer.

Tack för förklaringen! Undrar bara varför man får arean som om man hade räknat med radianer när man räknar med papper och penna genom att ta fram den primitiva funktionen, även om man har använt grader? -cos(135*) + sin(135*) + cos(-45*) - sin(-45*) ger samma svar som om man använde radianer

Pankakan skrev:

genom att ta fram den primitiva funktionen, även om man har använt grader?  

Det är inte den primitiva funktionen.

Derivatan av $\sin \dfrac{2\pi}{360} x$ har en faktor $\dfrac{2\pi}{360}$ framför cosinus (kedjeregeln).

Pieter Kuiper skrev:

Pankakan skrev:

genom att ta fram den primitiva funktionen, även om man har använt grader?  

Det är inte den primitiva funktionen.

Derivatan av $\sin \dfrac{2\pi}{360} x$ har en faktor $\dfrac{2\pi}{360}$ framför cosinus (kedjeregeln).

Varför används sin ((2π/360)*x) istället för bara sin x? Beror det på något med att radianer måste användas när man tex deriverar sinus och cosinus funktioner?

Pankakan skrev:

Beror det på något med att radianer måste användas när man tex deriverar sinus och cosinus funktioner?

Det är i alla fall starkt rekommenderat, för annars får man mycket strul.