Olikheter
Varför är B det rätta svaret? Om man tar roten ur båda sidorna får man inte ±y > ±2, eller? Nu är jag lost...

Att y2 > 4 innebär att antingen är y < -2 eller så är y > 2.
Är du med på det?
Yngve skrev:Att y2 > 4 innebär att antingen är y < -2 eller så är y > 2.
Är du med på det?
Hur blev det y < -2? Varför vände du på olikhetstecknet?
Att y2 > 4 innebär att y är tillräckligt långt bort från 0 så att kvadraten av y är större än 4.
Om y t.ex. är -1 så är y2 = (-1)2 = 1, vilket är mindre än 4.
Alltså kan inte y > -2 vara en lösning.
Yngve skrev:Att y2 > 4 innebär att y är tillräckligt långt bort från 0 så att kvadraten av y är större än 4.
Om y t.ex. är -1 så är y2 = (-1)2 = 1, vilket är mindre än 4.
Alltså kan inte y > -2 vara en lösning.
Så y2 kan t.ex. vara -3, y2 > (-3)2. I det fallet så är y < x (vilket är 2) och då kan inte B vara sann.
OmarTaleb skrev:
Så y2 kan t.ex. vara -3,
Nej. Men om du menar att y kan vara lika med-3 så stämmer det.
y2 > (-3)2. I det fallet så är y < x (vilket är 2) och då kan inte B vara sann.
Vi vet att x 2. Der betyder att x kan vara lika med 2 eller att x kan vara lika med -7.
Eftersom y t.ex. kan vara lika med -3 så kan vi inte säga vilket av x och y som är störst.
Yngve skrev:OmarTaleb skrev:Så y2 kan t.ex. vara -3,
Nej. Men om du menar att y kan vara lika med-3 så stämmer det.
y2 > (-3)2. I det fallet så är y < x (vilket är 2) och då kan inte B vara sann.
Vi vet att x 2. Der betyder att x kan vara lika med 2 eller att x kan vara lika med -7.
Eftersom y t.ex. kan vara lika med -3 så kan vi inte säga vilket av x och y som är störst.
För att vara så tror jag inte att jag har fattat något hittills.
Det jag förstår är att y2 > 4. Om man tar roten ur båda leden så får man ±y > ±2, eller är det ±y > 2?
OmarTaleb skrev:Det jag förstår är att y2 > 4. Om man tar roten ur båda leden så får man ±y > ±2, eller är det ±y > 2?
Det sistnämnda, dvs , dvs antingen är eller så är (vilket är samma sak som att ).
Du kan även se detta grafiskt.
Rita parabeln , den ser ut så här:
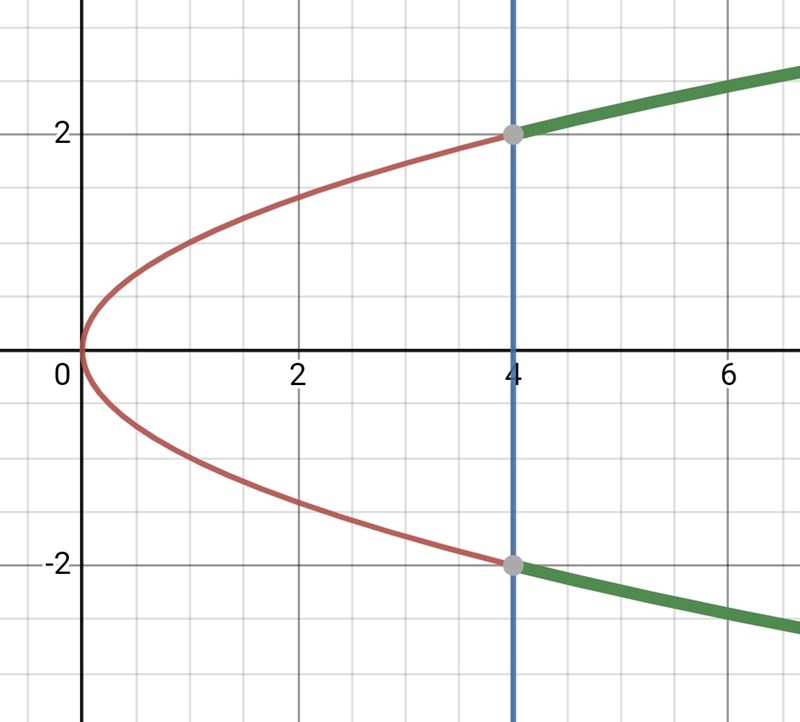
Jag har ävwn ritat linjen och fyllt i den delen av parabeln som uppfyller med tjockare grön färg.
Du ser där att villkoret är uppfyllt dels för , dels för .
Yngve skrev:OmarTaleb skrev:Det jag förstår är att y2 > 4. Om man tar roten ur båda leden så får man ±y > ±2, eller är det ±y > 2?
Det sistnämnda, dvs , dvs antingen är eller så är (vilket är samma sak som att ).
Du kan även se detta grafiskt.
Rita parabeln , den ser ut så här:
Jag har ävwn ritat linjen och fyllt i den delen av parabeln som uppfyller med tjockare grön färg.
Du ser där att villkoret är uppfyllt dels för , dels för .
Så y kan ha två värden, antingen 2 eller -2. Men i själva frågan så skriver de bara y och frågar ifall x eller y är större. Jag menar att y har 2 värden, hur ska jag veta vilken jag ska använda? (av den anledningen valde jag alternativ D i frågan).
Vi får inte veta mer om y, så y kan vara antingen 2 eller -2, och då kan vi inte säga att någon av A-C är sann, så det är D.
Laguna skrev:Vi får inte veta mer om y, så y kan vara antingen 2 eller -2, och då kan vi inte säga att någon av A-C är sann, så det är D.
Jag tänker samma, men enligt bilden så är det rätta svaret B :/
Få se nu här:
Två möjliga värden på x & y som stämmer in på beskrivningen är att x= 2, y= -1 000 000. 2 > -1 000 000 så då är x större än y.
Två andra möjliga värden är att x= 2, y= 1 000 000. 2 < 1 000 000 så då är y större än x.
Jag vill därmed ha svaret till D. Var har du fått den här uppgiften från?
OmarTaleb skrev:
Så y kan ha två värden, antingen 2 eller -2.
Nej, y kan ha vilket värde som helst som är nindre än -2 eller större än 2. Det är precis det som olikheten betyder.
Men i själva frågan så skriver de bara y och frågar ifall x eller y är större.
På samma sätt: kan ha vilket värde som helst som är mindre än eller lika med 2. Det är precis det som olikheten betyder (då ).
Jag menar att y har 2 värden, hur ska jag veta vilken jag ska använda? (av den anledningen valde jag alternativ D i frågan).
Alternativ D är rätt, eftersom det enligt ovan inte går att säga huruvida är större ön, mindre än eller lika med .
Exempel som påvisar detta:
- Det finns inget I olikheterna som hindrar att t.ex. och , vilket skulle betyda att .
- Men det finns heller inget som hindrar att t.ex. och , vilket skulle betyda att .
- Det finns heller inget som hindrar att t.ex. både och är lika med -10, vilket skulle betyda att



