Olikheter av taylorutvecklingar
Hej!
Vad är bästa metoden för att avgöra om sådana här olikheter stämmer eller inte:
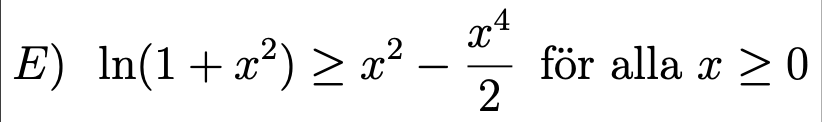
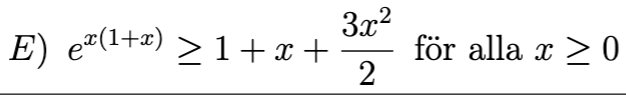
?
Fann ej någon Taylorlösning till den första.
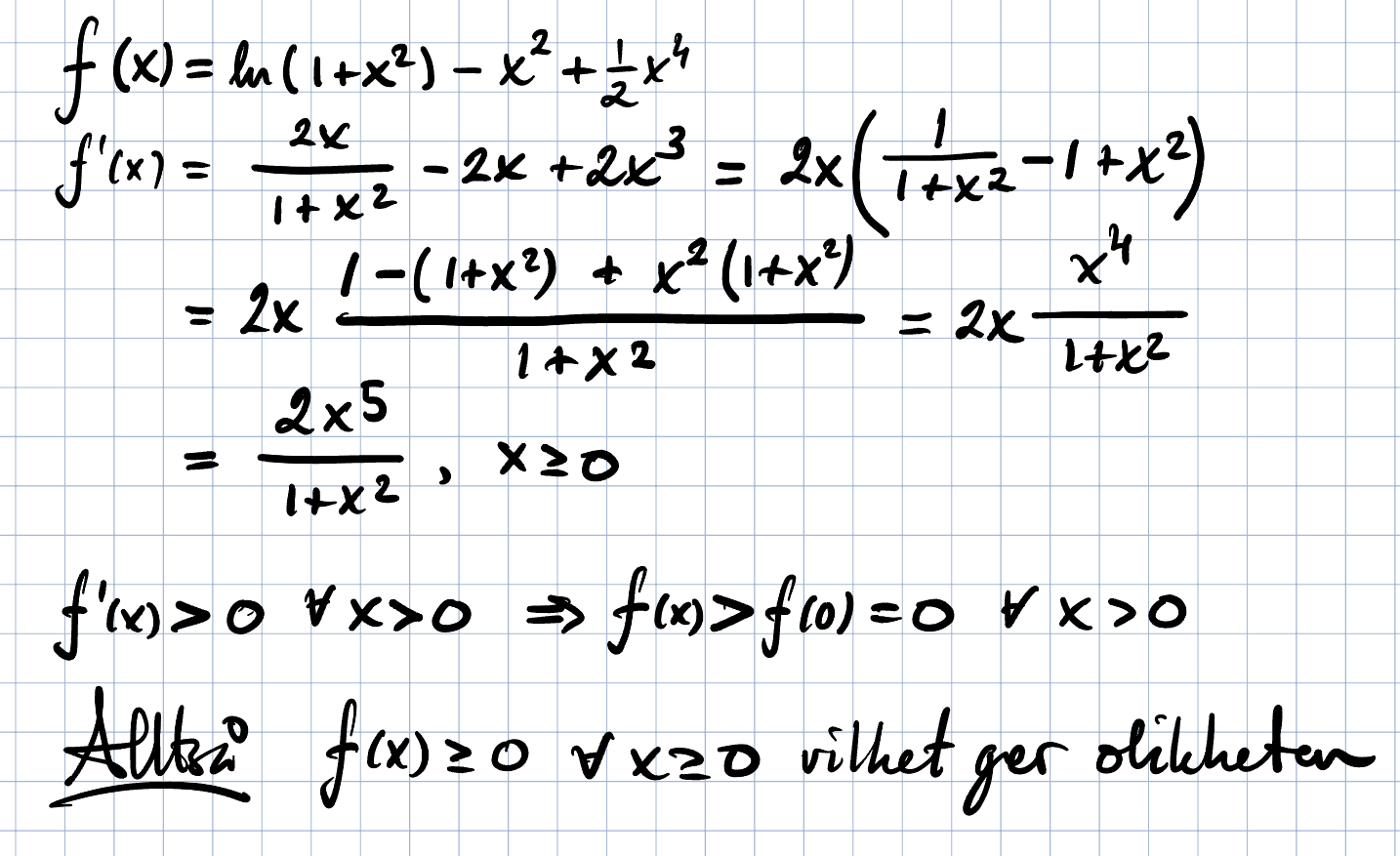
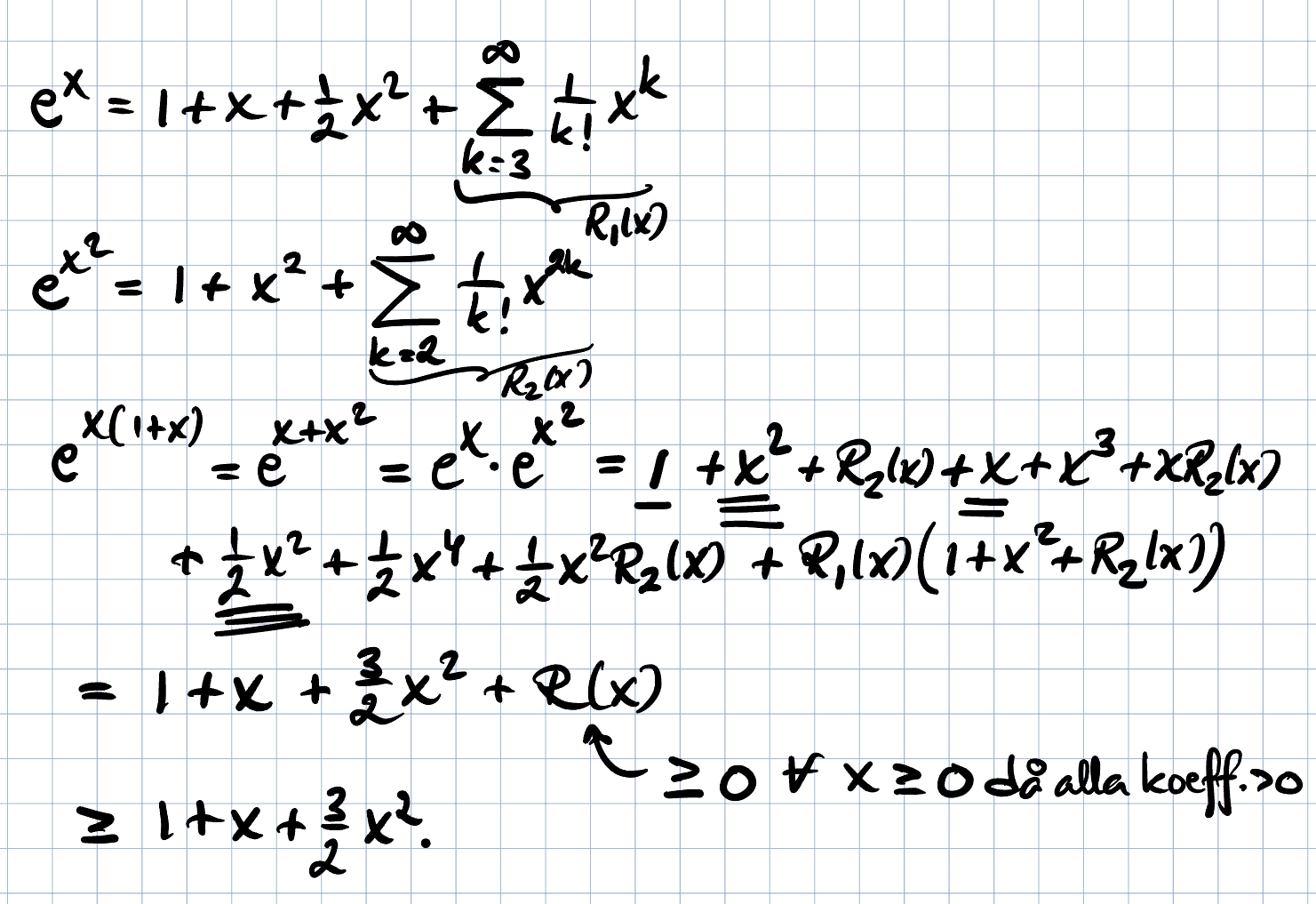
Snygga lösningar! Är det de alternativen man har?
Detta är en lösning med taylor på första. Den var mycket bökigare:

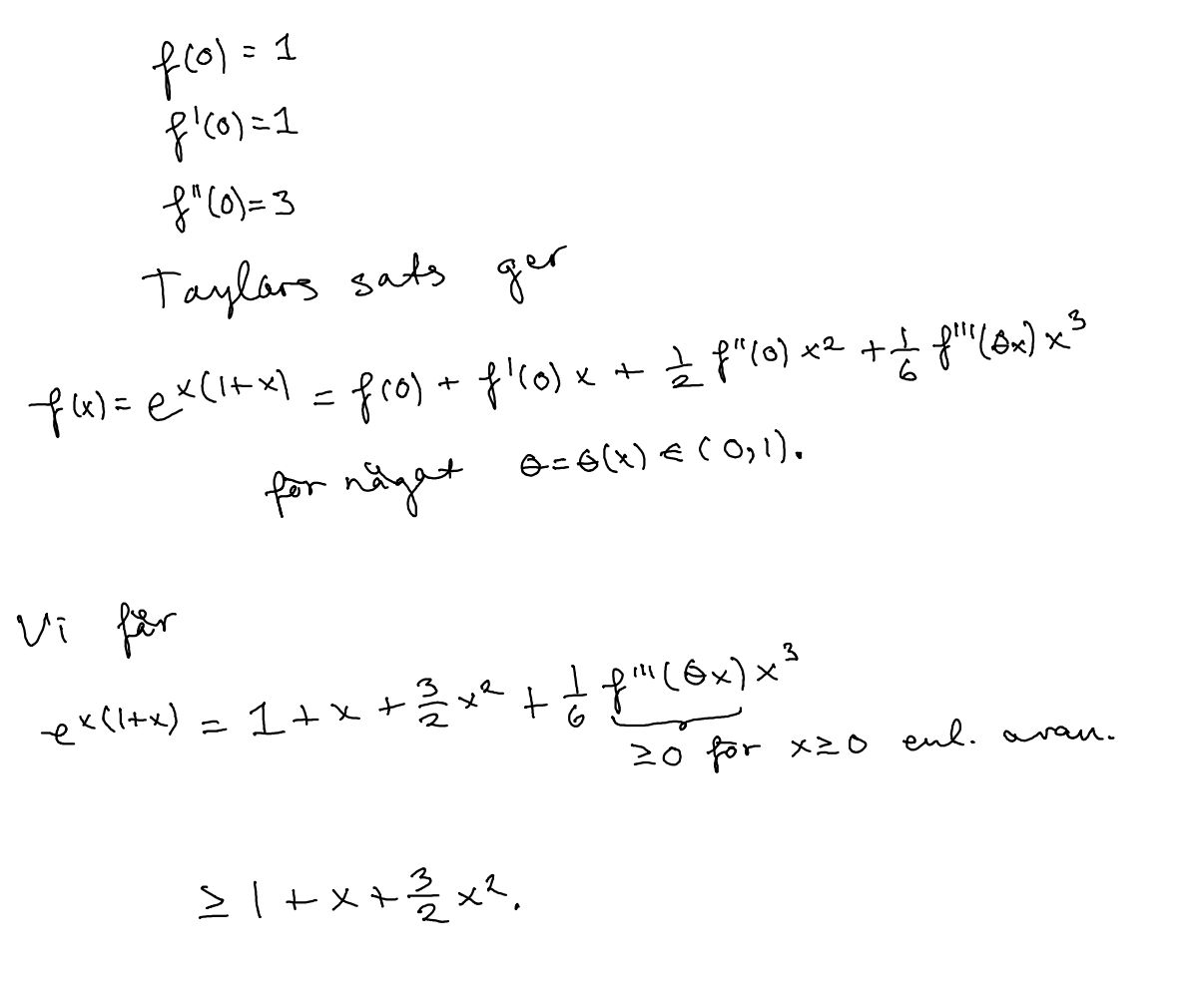
MrPotatohead skrev:Snygga lösningar! Är det de alternativen man har?
Detta är en lösning med taylor på första. Den var mycket bökigare:
Se bra ut! (men du menar nog andra uppgifen)
Jag tänkte först att man skulle T-utv. ln(1+x^2) men den är alternerande och det är inte självklart att resttermen är ≥0. En "gymnasieanalys" funkade dock här.
Aa oj, hehe, kollade fel. Ja, det är tufft när det blir alternerande. Får hoppas att derivatan fungerar om den dyker upp.
MrPotatohead skrev:Aa oj, hehe, kollade fel. Ja, det är tufft när det blir alternerande. Får hoppas att derivatan fungerar om den dyker upp.
Man kan göra som du, utv x(x+1) och ta det som inargument till serien för e^x. Dock tror jag man bör öva "multiplikation" som jag visar ovan då provkonstruktörer älskar hitta på de mest patologiska produkter och kvoter vars gränsvärde skall bestämmas. Det krävs lite övning i att multiplicera polynom och resttermer "så det går undan" (det mesta försvinner när gradtalet ökar bortom rim och reson) så det kan vara bra om du övar på det också. 98% av alla termer kan man "kasta bort" (eller gruppera i en ny restterm) och det är denna "känsla" som är bra att öva in. Notera hur jag (pedagogiskt) börjar med att skriva produkterna men på slutet slänger jag bara till med R(x) eftersom alla de produkterna har högre gradtal än 2.




