Olikheter med absolutbelopp
Jag vet att abs(2x-3) = 2x - 3 om x>3/2 och -(2x-3) om x < 3/2
och att abs(1-x )= 1-x om x>1 och -(1-x) om x<1
dock är jag osäker om hur jag ska fortsätta
Bra början!
Ett sätt att fortsätta är grafisk lösning: Rita graferna y = |2x-3| och y = |1-x|. Då ser du direkt vilka x-värden som ger lösningen.
Ett annat sätt är en algebraisk lösning: Dela då upp problemet i de tre områdena , och .
Ersätt absolutbelopputtrycken med deras motsvarighet utan absolutbelopptecken i respektive intervall.
Du får då tre enklare olikheter att lösa. Men du måste kontrollera att respektive lösning är giltig i aktuellt intervall.
Yngve skrev:Bra början!
Ett sätt att fortsätta är grafisk lösning: Rita graferna y = |2x-3| och y = |1-x|. Då ser du direkt vilka x-värden som ger lösningen.
Ett annat sätt är en algebraisk lösning: Dela då upp problemet i de tre områdena , och .
Ersätt absolutbelopputtrycken med deras motsvarighet utan absolutbelopptecken i respektive intervall.
Du får då tre enklare olikheter att lösa. Men du måste kontrollera att respektive lösning är giltig i aktuellt intervall.
mellan 1 < x < 3/2 ska högerleder vara -(2x-3) och vänsterledet 1-x ?
Koizenu skrev:Yngve skrev:Bra början!
Ett sätt att fortsätta är grafisk lösning: Rita graferna y = |2x-3| och y = |1-x|. Då ser du direkt vilka x-värden som ger lösningen.
Ett annat sätt är en algebraisk lösning: Dela då upp problemet i de tre områdena , och .
Ersätt absolutbelopputtrycken med deras motsvarighet utan absolutbelopptecken i respektive intervall.
Du får då tre enklare olikheter att lösa. Men du måste kontrollera att respektive lösning är giltig i aktuellt intervall.
mellan 1 < x < 3/2 ska högerleder vara -(2x-3) och vänsterledet 1-x ?
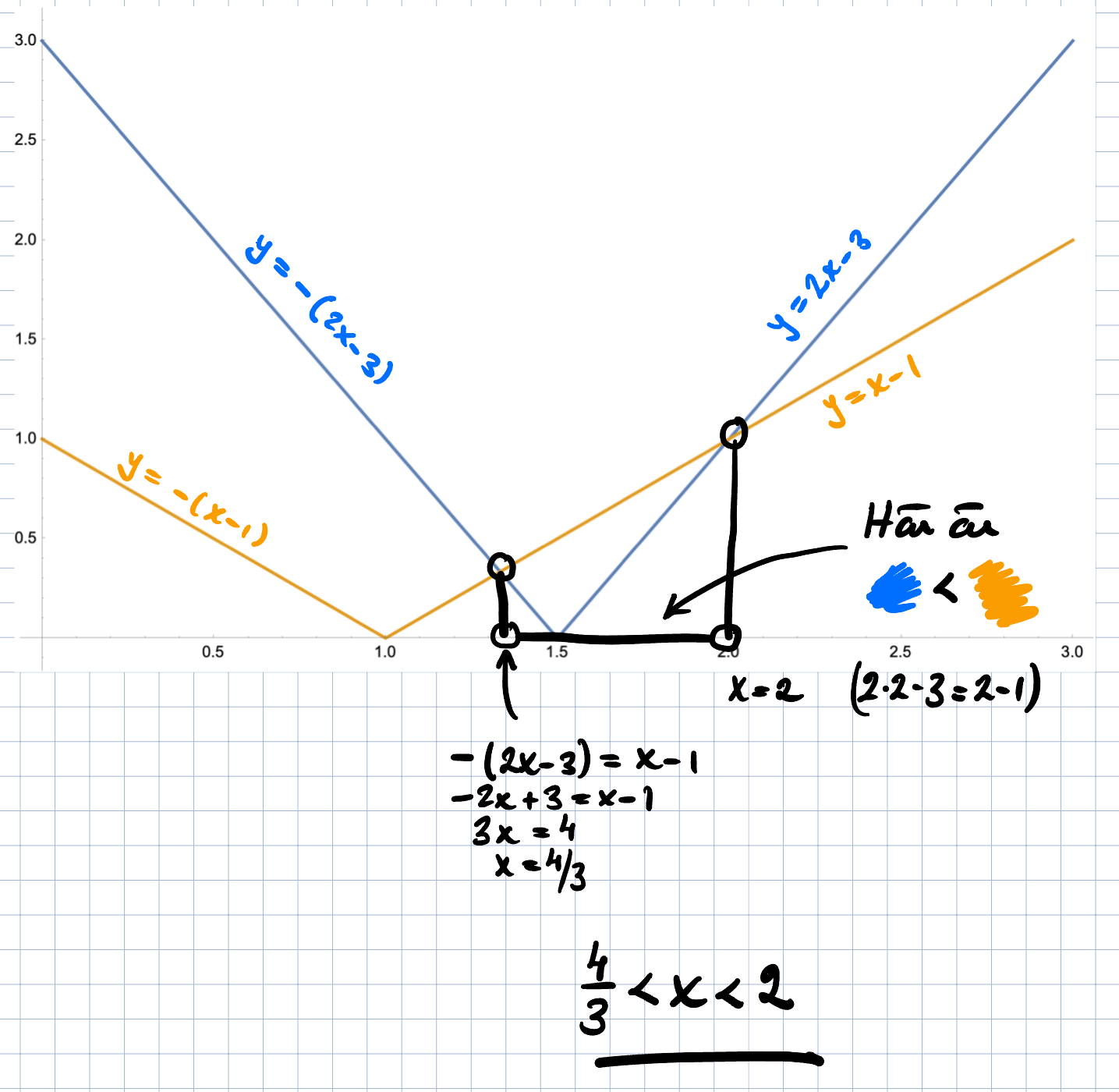
Koizenu skrev:
mellan 1 < x < 3/2 ska högerleder vara -(2x-3) och vänsterledet 1-x ?
- Intervall 1: . Här är |2x-3| = -(2x-3) och |1-x| = 1-x
- Intervall 2: . Här är |2x-3| = -(2x-3) och |1-x| = -(1-x)
- Intervall 3: . Här är |2x-3| = 2x-3 och |1-x| = -(1-x)


