Olikheter och absolutbelopp, förstår inte innebörden av x<x-6 och x>x-6 vid två fall.

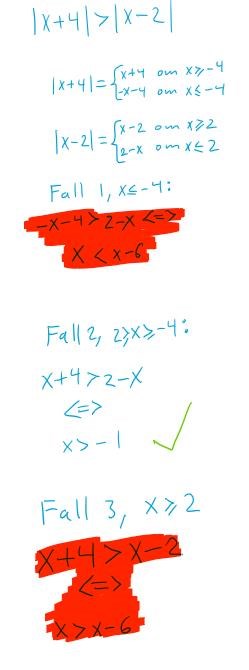
|x+4| är alltid positivt.Antingen så gäller det att |x+4|  = x+4 eller att |x+4| =-(x+4) = -x-4.

Om x<-4 så måste |x+4| = -x-4.

Det gäller likadant för den andra olikheten.

Som vanligt är det en bra idé att rita. I det här fallet blir det två v-formade figurer vär minimipunkterna är (-4,0) respektive (2,0) och lutningarna är 1 och -1. I vilka intervall ligger vilken av kurvorna överst?

Om lösningen är mindre än fyra är båda uttrycken negativa (innanför absolutbeloppen). Därför måste vi multiplicera båda uttryck med -1 för att kunna ta bort absolutbeloppen. Då får vi: 

$-\left(x+4\right)>-(x-2)$

Detta kan förenklas till: 

$-x-4>2-x$

Här blir det knasigt dock. Genom att flytta alla x till samma sida, får vi: 

$$\begin{gathered} -x-4+4>2-x+4 \\ -x>6-x \end{gathered}$$

Vi kan multiplicera båda led med -1, men då måste vi vända på olikhetstecknet.

Vi får:

$x<x-6$

Vilket vi kan möblera om till $0<-6$, vilket inte stämmer. Det finns med andra ord ingen lösning som är mindre än eller lika med -4. :)

Prova gärna att applicera samma metod på fall 3, och se om det blir lite tydligare. :)

Kan man tolka det som att i fall 1, då x<4 så är uttrycket |x+4| > |x-2| aldrig sant, medan det alltid är sant i fall 3, alltså för alla x>2?

Tips som kanske hjälper att förstå:

Plotta samtliga uttryck i grafräknaren eller geogebra:

|x+4|>|x-2|

|x+4|

|x-2|

Uttrycket |x+4|>|x-2| kommer ge antingen 1 eller 0 där 1 är sant och 0 är falskt. |x+4| och |x-2| kommer ge v-formade figurer som Smaragdalena skrev. Jämför de tre figurerna med varandra med åtanke att |x+4| ska vara större än |x-2|.

Hoppas det hjälper.

Om du ritar (så som jag beskrev) så ser du snabbt att olikheten är sann för alla x>-1. Olikheten är alltså inte sann för något värde som är mindre än -4.

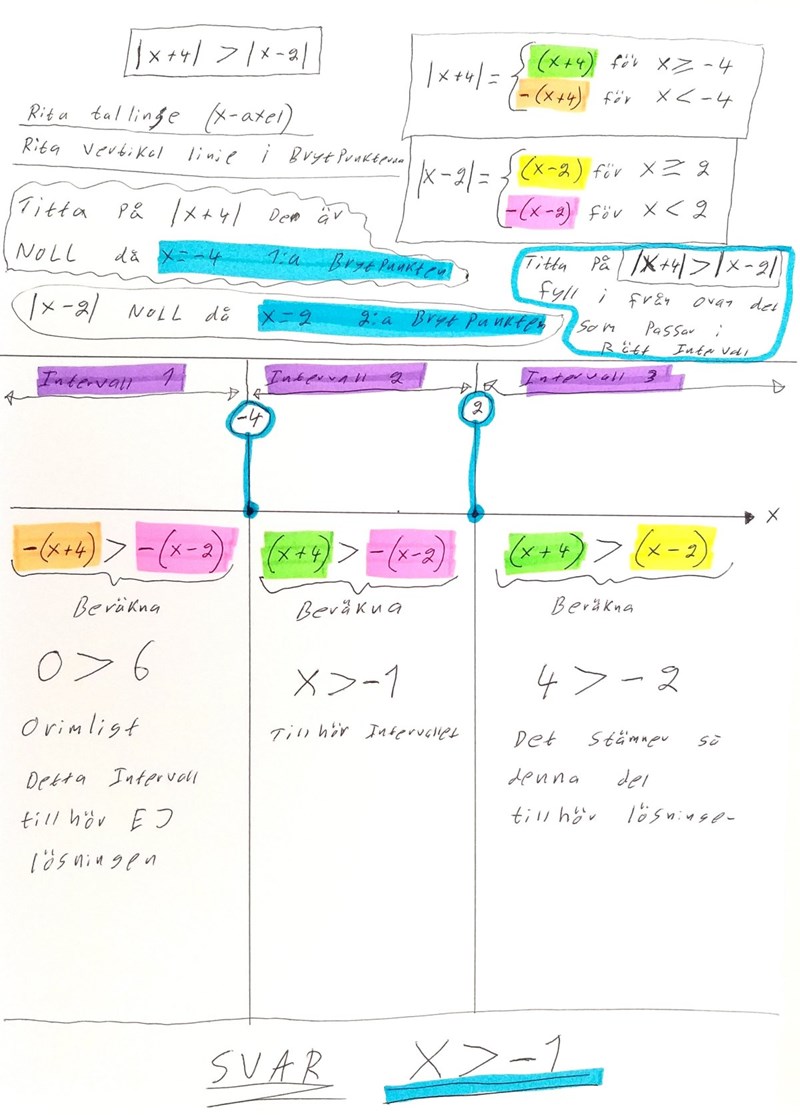
Altså: Intervall 1 tillhör Ej Lösningen. Första halvan av Intervall 2 tillhör Ej lösningen, men andra halvan av Intervall 2 X>-1 tillhör lösningen. samt Intervall 3

Hej Exoth,

Fall 1. Här är $x\leq -4$ och olikheten säger att avståndet mellan $x$ och -4 är större än avståndet mellan $x$ och 2. Detta är förstås nonsens, varför olikheten saknar lösningar på intervallet $(-\infty,-4]$.

Albiki skrev:

Hej Exoth,

Fall 1. Här är $x\leq -4$ och olikheten säger att avståndet mellan $x$ och -4 är större än avståndet mellan $x$ och 2. Detta är förstås nonsens, varför olikheten saknar lösningar på intervallet $(-\infty,-4]$.

Om du sätter in x = -3 tillhör den lösningen?

Niro skrev:

Albiki skrev:

Hej Exoth,

Fall 1. Här är $x\leq -4$ och olikheten säger att avståndet mellan $x$ och -4 är större än avståndet mellan $x$ och 2. Detta är förstås nonsens, varför olikheten saknar lösningar på intervallet $(-\infty,-4]$.

Om du sätter in x = -3 tillhör den lösningen?

Hej, Talet x=-3 är inte aktuellt vid Fall 1 eftersom -3 är större än -4, eller hur?

Albiki skrev:

Niro skrev:

Visa föregående citat

Albiki skrev:

Hej Exoth,

Fall 1. Här är $x\leq -4$ och olikheten säger att avståndet mellan $x$ och -4 är större än avståndet mellan $x$ och 2. Detta är förstås nonsens, varför olikheten saknar lösningar på intervallet $(-\infty,-4]$.

Om du sätter in x = -3 tillhör den lösningen?

Hej, Talet x=-3 är inte aktuellt vid Fall 1 eftersom -3 är större än -4, eller hur?

Hej, ja jag vet men jag gissar att om han har problem att förstå intervallen så kan han ha problem med lösningen i stort. I min bild kan man ju få uppfattningen att lösningen startar vid större än -4, men jag har redigerat texten och lagt till att så är inte fallet.

För tredje gången: Rita!

Som vanligt är det en bra idé att rita. I det här fallet blir det två v-formade figurer vär minimipunkterna är (-4,0) respektive (2,0) och lutningarna är 1 och -1. I vilka intervall ligger vilken av kurvorna överst?