Om ngn vill dubbelkolla min antiderivata?
P = e^{x^2} + x^2y
Q = y^2+sin(y)
dQ/dx = y^2x+(hur blir de thär med sin(y) ?)
dP/dy = e^{x^2} + x^2y^2/2
Stämmer verkligen detta?
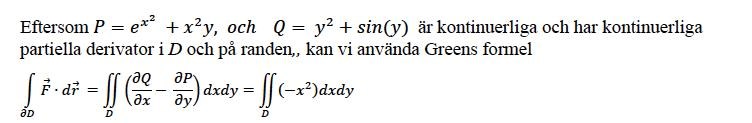
heymel skrev:P = e^{x^2} + x^2y
Q = y^2+sin(y)dQ/dx = y^2x+(hur blir de thär med sin(y) ?)
dP/dy = e^{x^2} + x^2y^2/2Stämmer verkligen detta?
Nej.
Eftersom Q inte beror av x så är dQ/dx = 0
Eftersom P endast beror av y genom termen x^2*y så är dP/dy = x^2
Dessa är partiella derivator, inte antiderivator (som ju är ett annat namn för primitiv funktion)
Yngve skrev:heymel skrev:P = e^{x^2} + x^2y
Q = y^2+sin(y)dQ/dx = y^2x+(hur blir de thär med sin(y) ?)
dP/dy = e^{x^2} + x^2y^2/2Stämmer verkligen detta?
Nej.
Eftersom Q inte beror av x så är dQ/dx = 0
Eftersom P endast beror av y genom termen x^2*y så är dP/dy = x^2
Dessa är partiella derivator, inte antiderivator (som ju är ett annat namn för primitiv funktion)
Men åååååh neeeej, fan, jaa så klart. ååååh... tänkte helt helt helt galet. Fattar inte varför jag antideriverade när det fan står klart & tydligt d för derivate, suck...


