Omvandling mellan talsystem
Hej! Jag ska omvandla det oktala talet 526,5 till det binära talsystemet.
Först omvandlar jag talet till det decimala talsystemet och från det omvandlar jag det till det binära talsystemet. Metoden har fungerat för alla heltal men stött på ett problem när decimaler är involverade.
För att få ett binärt tal måste väl resterna vara 1 eller 0, men jag får den första resten till 0,625. Vad gör jag för fel?
När det är decimaler får man multiplicera med basen i stället. 0,5 * 8 = 4. Så den delen blir 0,4 oktalt.
Där hängde inte jag med, Bråkdelen 0,5 är väl oktal den också?
Decimalt blir den 5*8^(-1) = 5*2^(-3) = (1 + 2^2)*2^(-3) = 2^(-1) + 2^(-3)
Binärt blir det 0,101.
Jaha, det var oktalt och skulle bli binärt. Då gjorde jag något annat än man skulle.
Då kan man ta en oktal siffra i taget och skriva den binärt, med tre binära siffror.
Laguna skrev:Jaha, det var oktalt och skulle bli binärt. Då gjorde jag något annat än man skulle.
Då kan man ta en oktal siffra i taget och skriva den binärt, med tre binära siffror.
Jag förstår inte. Hur gör man det?
Jag får rätt när jag skriver om 342 från decimalt till binär men förstår inte hur jag ska göra med 0,625. Försökte lösa det som ett ”eget tal” men det blev helt fel.
Laguna skrev:Jaha, det var oktalt och skulle bli binärt. Då gjorde jag något annat än man skulle.
Då kan man ta en oktal siffra i taget och skriva den binärt, med tre binära siffror.
Vänta det fungerar om jag adderar det binära talet jag fick från 625.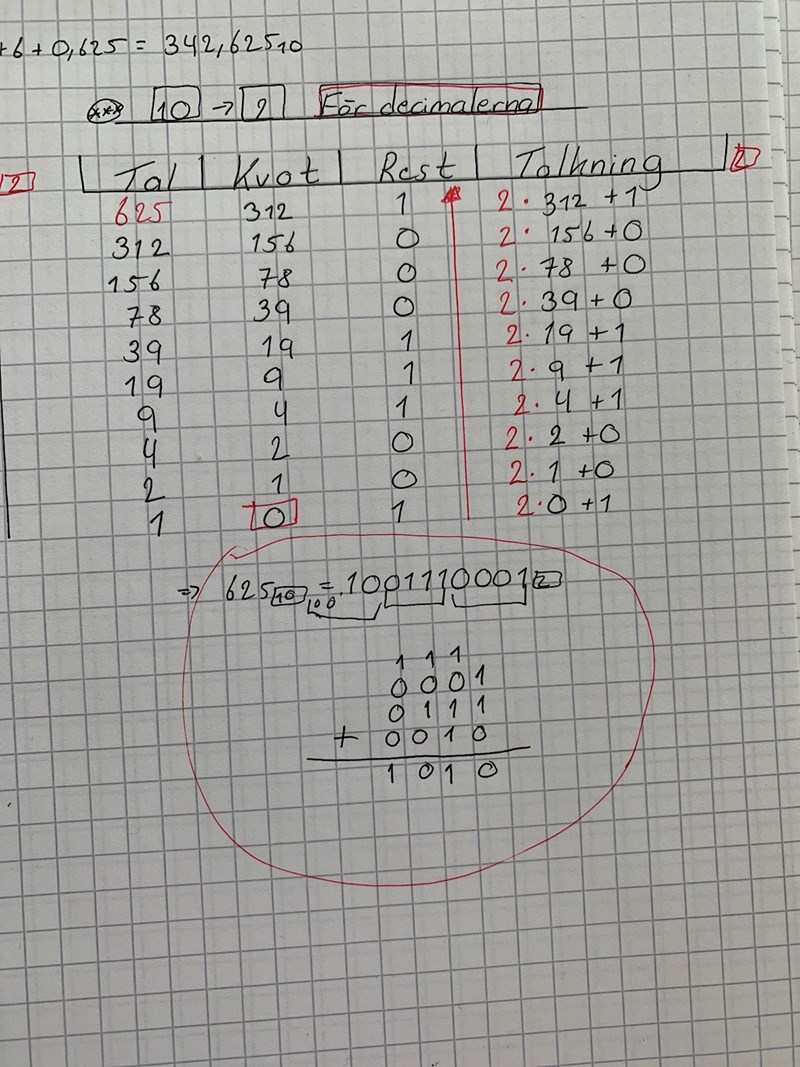
Då får jag rätt decimaler. Råkade det bara bli rätt eller kan jag faktiskt göra så?
Det måste vara en tillfällighet. Prova med något annat tal.
Sättet man använder när man ska omvandla decimaler till en annan bas är att man multiplicerar med basen, får en siffra, tar bort den, multiplicerar igen, osv. tills det tar slut. (Eller kanske aldrig tar slut, men då ser man ett mönster.)
0,625 * 2 = 1,25 vi fick 1, ta bort den
0,25 * 2 = 0,5 vi fick 0
0,5 * 2 = 1,0 vi fick 1, och tar vi bort den är det 0 och slut
Så vi fick de binära decimalerna 1 0 1
Det jag skrev om oktalt och tre binära siffror är så här: man kan ta en oktal siffra i taget och skriva den binärt (alltid med tre siffror, dvs. kanske med nollor först), och sedan är man klar: 526,58 = 101 010 110, 101
Det här fungerar bara för att tre binära siffror precis motsvarar en oktal siffra (8 är en potens av 2). Det fungerar inte med t.ex. binärt och 10.



