Optimering

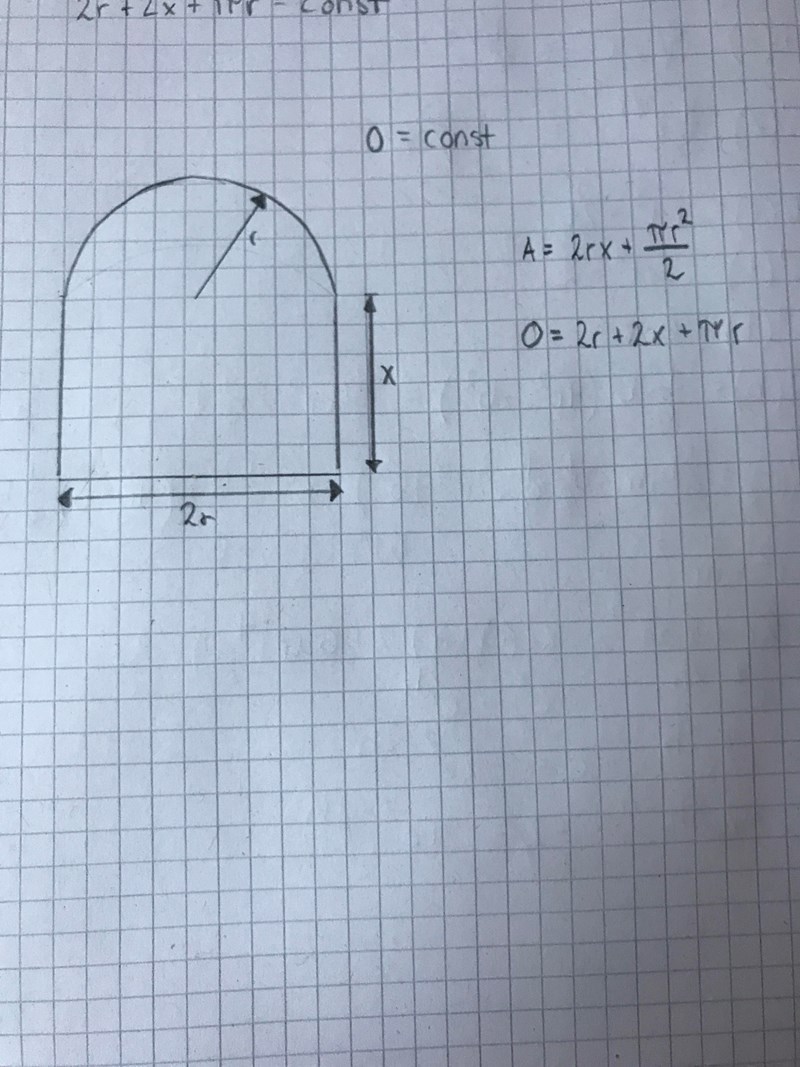
Jag misstänker att det står nåt mer i uppgiften. T.ex.  nåt samband mellan x och r. 

Nej faktiskt inte

Det här ser ut som en typisk Ma3-uppgift. Jag flyttar tråden dit från Matematik/Universitet. /moderator

Skriv x som en funktion av r, skriv arean som en funktion av (endast) r, derivera och sätt derivatan lika med 0. Standarduppgift.

Vad menas med skriv x som en funktion av r?

Linnimaus skrev:

Nej faktiskt inte

Då sätter jag r och x till 700 ljusår. Är nån inte nöjd så multiplicerar jag med 10.

Ska kanske omkretsen vara konstant eller något?

Ja det står ju på pappret

Linnimaus skrev:

Ja det står ju på pappret

Finns x och r i den?

Egocarpo skrev:

Linnimaus skrev:

Ja det står ju på pappret

Finns x och r i den?

Som sagt på bilden jag har postat står allt.

Linnimaus skrev:

Egocarpo skrev:

Visa föregående citat

Linnimaus skrev:

Ja det står ju på pappret

Finns x och r i den?

Som sagt på bilden jag har postat står allt.

Kolla där då? Det syns väldigt dåligt på bilden.

är det noll= konstant eller bokstaven O vilket kan beteckna omkretsen som är konstant?

Linnimaus skrev:

Ja det står ju på pappret

Jaha, jag läste bara texten. Då finns det alltså ett samband mellan r och x. Då gör du som Smaragdalena föreslog. 

Det finnns tillräckigt med info i uppgiften för att man skall kunna lösa den.

Egocarpo skrev:

Linnimaus skrev:

Ja det står ju på pappret

Finns x och r i den?

Ganska högt upp står det O=const vilket torde betyda att omkretsen är konstant och lite längre ner står det O=2r+2x+$\pi$r. Det är enkelt att att lösa ut x ur denna ekvation och sätta in uttrycket i uttrycket för arean.

Vad menas med skriv x som en funktion av r?

Lös ut variablen x ur uttrycket O=2r+2x0$\pi$r, precis som du lärde dig i Ma1.

Ser det ens någorlunda rätt ut? Har ingen aning vad jag håller på med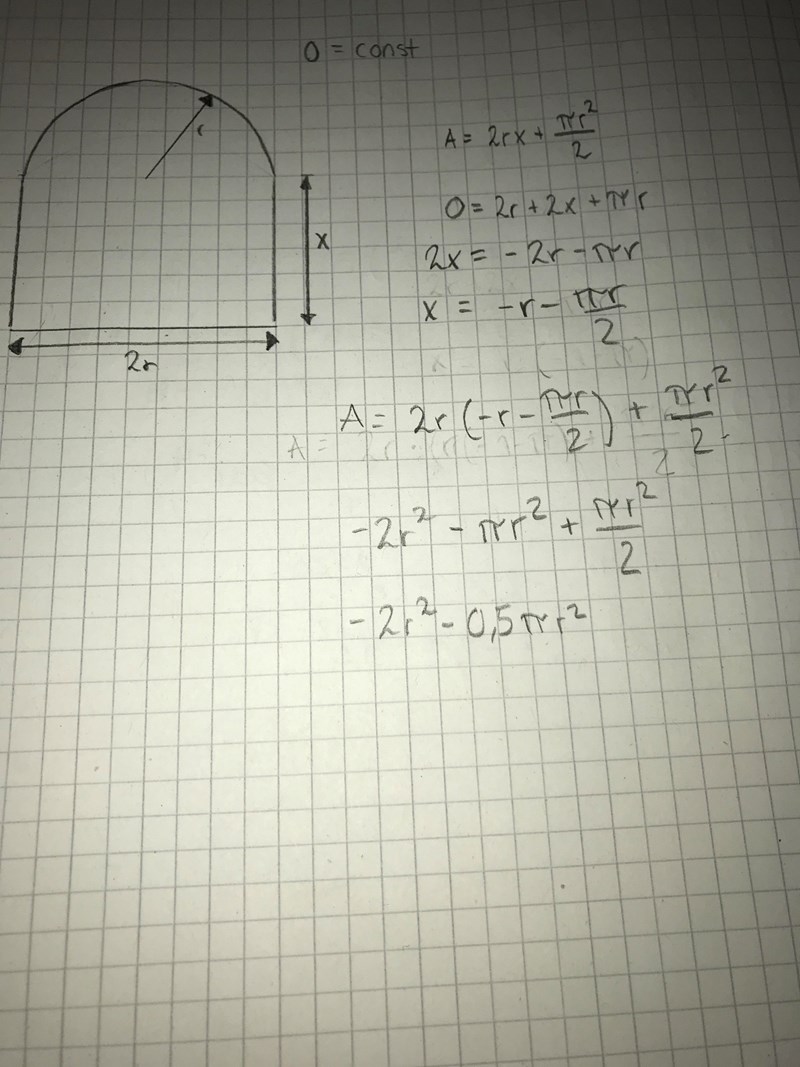

Var det noll och inte omkretsen nu? O=2r+2x+/pi*r

Inte noll utan omkretsen

O=2r+2x+pi*r får du till 2x=-2r -pi*r hur sker detta om det är O i början och inte noll?

Ska det kanske vara 2x= O -2r -pi*r

Nä men det är ju just det jag inte förstår. Hur jag ska lösa ut x eller r....

Jag är ett steg ifrån att lösa ut x i denna. Dela med två på båda sidor så har du löst ut x. O är bara ett tal som får vara med i svaret.

Edit; x= O/2 -r -pi*r/2 Sedan stoppa in detta i area formeln och derivera.

Ok jag ger upp nu. Fattar verkligen inte.

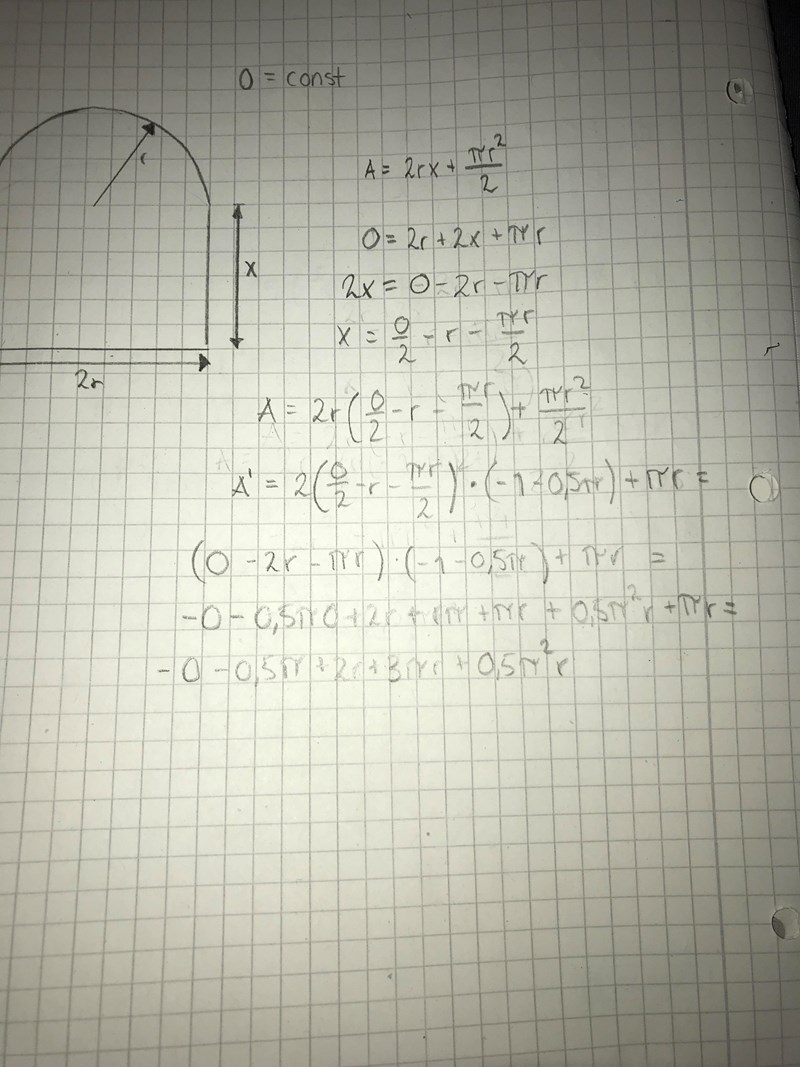
Du är nästan där. Antingen får du multiplicera in 2r innanför parentesen innan du deriverar eller så blir det en produkt regel.

Om du multiplicerar in A=O*r-2*r²-pi*r²+pi*r²/2 => A'(r)=O-4*r-pi*r*2+pi*r= O+r(-4-2*pi+pi)=O+r(-4-pi)= noll

=> r = -O/(-4-pi)=O/(4+pi) , där O är omkretsen som är en konstant.

Det är sent men detta är ett försök. :)

Fint! Jag har kommit till samma resultat.

Intressant att finna att r(opt) = x(opt). Båda är lika med p/(4+π).

Här har jag betecknat omkretsen (perimetern) med  p  för att slippa de missförstånd som lätt uppstår om man betecknar den med O. I handskrift går det ju knappast att skilja O från en nolla.  Varför skulle man då någonsin välja O som beteckning för en numerisk storhet?