Optimeringsproblem
Hej!
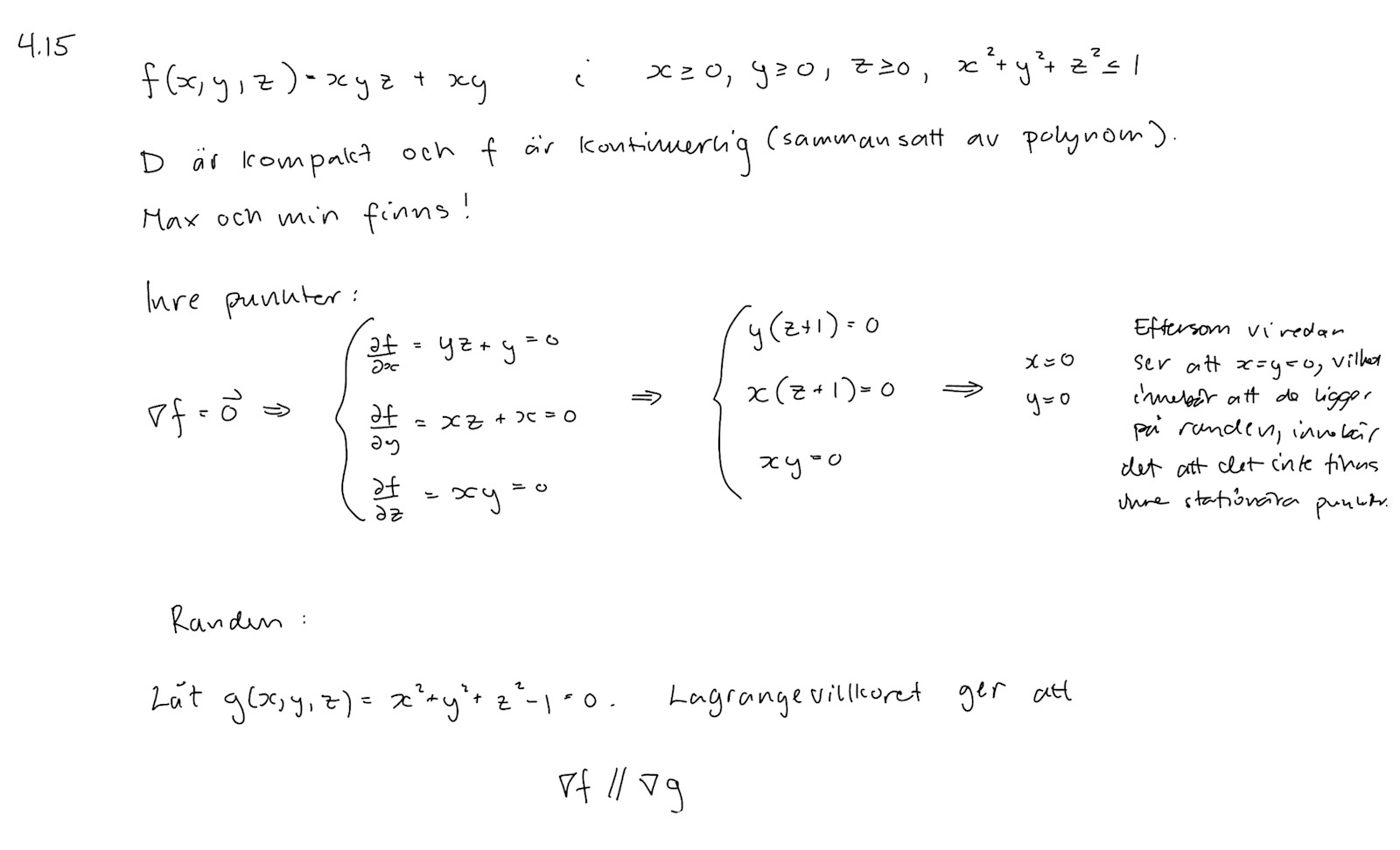
Jag har fastnat på hur jag ska hitta extrempunkter på randen. Är det jag har gjort innan rätt?
Randen är
(0) Hörnen
(1) dels tre plana kvartscirkelskivor där något av x, y eller z är 0 så den enda av dem som ger något är när z = 0 som ger f = xy,
(2) dels åttondelssfären med radie 1.
(0) Hörnen tror jag du fixar själv.
(1) Skivan i xy-planet tror jag också du klarar.
men (2) är intressant. Jag har inte löst den utan spånar medan jag skriver.
Om vi sätter
x = R cosu sinv
y = R sinu sinv
z = R cosv
Så är R = 1, 0 < u < 90o , 0 < v < 90o (detta bör kollas, länge sedan jag gjorde detta. Och det kan vara säkrare att skriva i radianer).
För ett obeväpnat öga ser det kanske inte jättelockande ut att derivera f-uttrycket med avseende på u och v, men det kanske finns sätt att förenkla det trigonometriska uttrycket.
Take it or leave it, lycka till.
Nu provade jag att angripa mitt polära uttryck. För den som gillar trigonometri är det en fest. Måste ses även om det inte ger något resultat!
Och det gick rätt bra med litet dubbla vinklar och att faktorisera derivatorna så att ekvationerna blev hanterliga, men mitt resultat blev märkligt. Kan ha gjort fel någonstans.
Jo, det funkade till sist. De rymdpolära koordinaterna kan man ta från början.
Du orkar kanske inte läsa detta men det blev så snyggt att jag måste publicera det.
x = R cosu sinv
y = R sinu sinv
z = R cosv
där 0 ≤ R ≤ 1, 0 ≤ u ≤ 90o , 0 ≤ v ≤ 90o
ger f = R3(cos sin …) + R2 (cos sin …)
I första oktanten är f uppenbart ≥ 0 och i origo är f = 0 så minsta värde fås genast till 0.
Vi ser också att om u och v hålls fixa så ökar värdet för f när R ökar, dvs största värde fås på åttondelssfären där R = 1.
Vi har alltså
x = cosu sinv
y = sinu sinv
z = cosv
0 ≤ u ≤ 90o , 0 ≤ v ≤ 90o som ger
f = cosu sinv sinu sinv cosv + cosu sinv sinu sinv
Det fina här är att u och v kan separeras så att deriveringen blir enkel.
f = [sin(2u) / 2] [sinv sinv cosv + sinv sinv]
df/du = … = cos(2u) sin2v (cosv +1) som bara är noll för u = pi/4
df/dv = … = [sin(2u) sinv] [2cos2v + 2cosv - sin2v]/2 där man får lösa ekv
cos2v + (2/3)cosv –1/3 = 0
som ger cosv = 1/3 samt sinv = (sqr8)/3
u = pi/4 ger cosu = sinu = (sqr2)/2
Insatt får vi (x, y, z) = (2, 2, 3)/3 och maximalt värde 8/9.
Minsta värde är 0 (i t ex origo).
(anm. Jag hoppade över fallen u = 0 som ger y = 0, och v = 0 som ger x = y = 0.
Båda innebär att f = 0.)
Insatt får vi (x, y, z) = (2, 2, 3)/3 och maximalt värde 8/9.
Rättelse: Ska vara
Insatt får vi (x, y, z) = (2, 2, 1)/3 och maximalt värde 16/27.


Fantastiskt bra hjälp! Tack så mycket. Här är min slutgiltiga lösning

