Optimeringsproblem rektangel i cirkel.
Behöver hjälp med att komma igång med denna frågan.
Bestäm arean av den största rektangel man kan skära ut ur en cirkulär plåtbit med radien R.
Jag började med att säga att arean är för rektangeln.
Sen vill jag försöka se något samband med cirkeln och rektangeln , funderade över om jag skall skriva y uttryckt i R och sedan sätta in i en funktion A(x) = xy
Eller hur skall jag börja ?
Sätt x=r.cos(v) och y=r.sin(v) där vinkeln v är i första kvadranten. Ställ upp uttrycket för arean, derivera och sätt derivatan lika med 0.
Behöver du mer hjälp si visa hur du har försökt och hur långt du ha kommit.
Det går säkert att räkna med x och y och använda sig av sambandet x2+y2=r2 också, men jag tror att det blir lättare att räkna som jag beskrev.
Smaragdalena skrev:Sätt x=r.cos(v) och y=r.sin(v) där vinkeln v är i första kvadranten. Ställ upp uttrycket för arean, derivera och sätt derivatan lika med 0.
Behöver du mer hjälp si visa hur du har försökt och hur långt du ha kommit.
Det går säkert att räkna med x och y och använda sig av sambandet x2+y2=r2 också, men jag tror att det blir lättare att räkna som jag beskrev.
Svaret skall i slutändan bli
Om jag säger att x=r*cos(v) och y=r*sin(v) kommer uttrycket då bli en funktion A(v) ? Är det den jag skall derivera ?
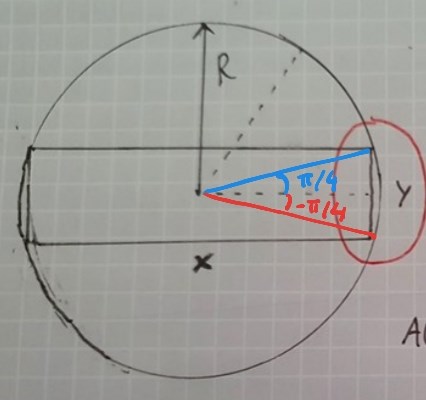
Det jag inte förstår är hur man kan säga att basen av rektangeln kan bli Rcos(v) respektive höjden som blir Rsin(v)?
Borde det inte bli 2Rcos(v) för basen eftersom man behöver 2 radier för att det skall bli x enligt bilden. Sen tänker jag även att det blir ju ett hålrum som jag ringat in med rött?
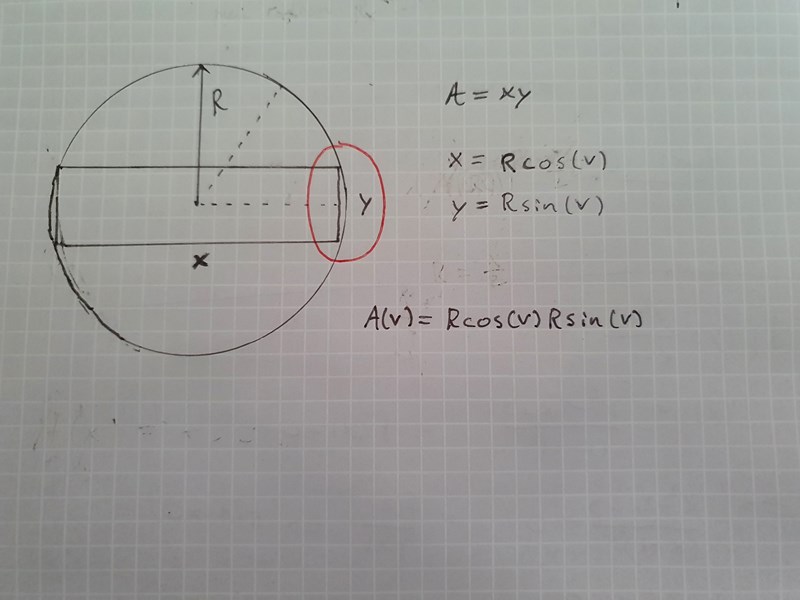
Smaragdalena menade att cirkeln är centrerad kring origo. Då blir koordinaterna (x,y) för rektangelns övre högra hörn (rcos(v), rsin(v)).
Arean blir då A = 2x*2y = 2rcos(v)*2rsin(v)
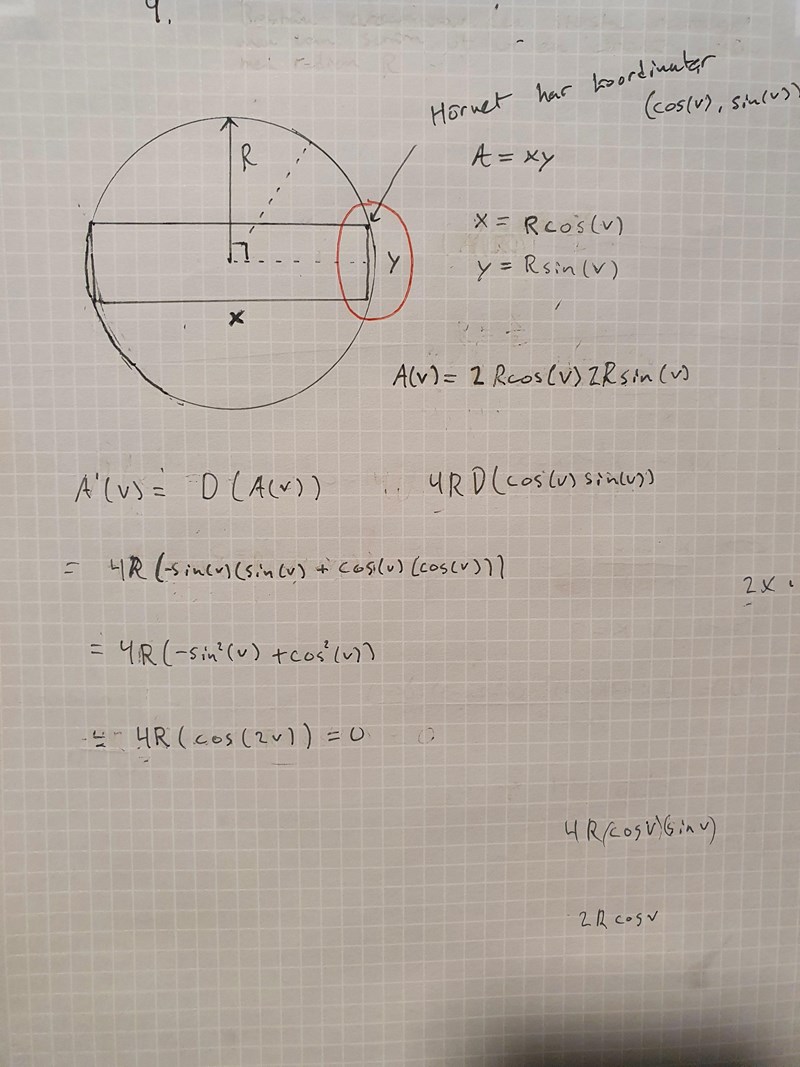
Jag använde mig utav uttrycket Yngve gav mig , deriverade och förenklade. Sätter derivata lika med noll.
Jag får då 4R(cos(2v))=0 , men hur skall jag bära mig åt för att lösa denna och få ett vettigt svar som jag sedan sätter in i min A(v) funktion, jag antar att jag skall lösa ut v men där skall väl R hänga med ?
Du har missat en faktor R.
Vi deriverar:
ger nu
Enligt nollproduktmetoden måste det då antingen gälla att (ointressant lösning) eller att
Att innebär att
Kommer du vidare härifrån?
Yngve skrev:Du har missat en faktor R.
Vi deriverar:
ger nu
Enligt nollproduktmetoden måste det då antingen gälla att (ointressant lösning) eller att
Att innebär att
Kommer du vidare härifrån?
Yes , tack så mycket.
Jag får rätt svar när jag sätter in pi/4 i A(v) , sen antar jag att man skippar -pi/4 för att man inte vill ha negativt tal på R.
Bra.
Vinkeln -pi/4 ger inte ett negativt värde på R.
Det motsvarar istället den rödmarkerade lösningen som kommer att ge samma resultat.
Det enklaste är ju att i själva modelleringen av problemet helt enkelt bestämma att eftersom detta intervall räcker för att hantera alla möjliga rektanglar som är inskrivna i en cirkel.
Sedan kanske man bör motivera varför just en inskriven rektangel ger den största arean.