Ordningen av snittet av två cykliska delgrupper (samt dess generatorer)

Hej!

Följande uppgift i min bok saknar facit och sålänge jag inte är dålig på att Googla så har ingen annan frågat om uppgiften online.

Biggs, Discrete Mathematics 20.9.3:

Suppose that $r$ and $s$ are divisors of $n$ , and the cyclic group $C_n$ is generated by $x$ . Write down generators for the cyclic subgroups $C_r$ and $C_s$ of $C_n$ . Find the order of $C_r \cap C_s$ , and write down a generator for this group.

Som jag så fint har fått förklarat för mig av Gustor i en annan tråd:

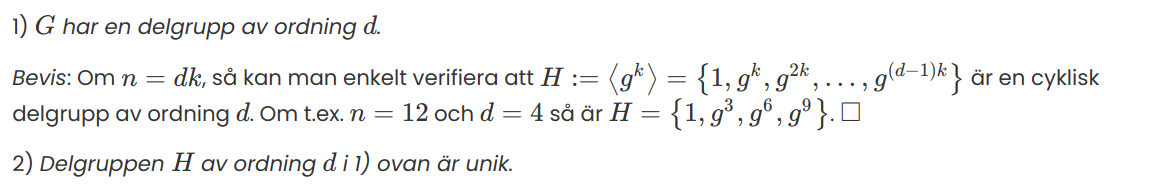
Utifrån denna förklaring kan jag dra slutsatsen att för t.ex. $C_r$ så borde generatorn vara $x^{\frac n r}$ om jag inte helt missförstått. Likaså får $C_s$ .

Men jag förstår inte riktigt hur jag ska hitta ordningen av $C_r \cap C_s$ . Jag misstänker att det har något att göra med att någon egenskap av elementen båda ska dela $r$ och $s$ . Kommer dock inte fram till något som är värt att visa upp för världen om man säger så. Kan jag få lite hjälp på traven?

Ledtråd: Låt $a=n/r$ och $b = n/s$ . Vi vet att $C_r = \langle x^a\rangle$ och att $C_s = \langle x^b\rangle$ från mitt förra inlägg.

Ett element i $C_r\cap C_s =\langle x^a\rangle \cap \langle x^b \rangle$ går att skriva både som $(x^a)^m$ och som $(x^b)^k$ för några heltal $m$ och $k$ . Det vill säga $x^{am} = x^{bk}$ . Med andra ord så är ett element i $\langle x^a\rangle \cap \langle x^b\rangle$ på formen $x^\ell$ där $\ell$ är delbart med både $a$ och $b$ , precis som du är inne på.

De heltal som är delbara med både $a$ och $b$ är precis de som är multiplar av $\operatorname{lcm} (a,b)$ . Jag hävdar nu att

$\langle x^a\rangle \cap \langle x^b\rangle = \langle x^{\operatorname{lcm} (a,b)}\rangle$ . (Vi kan visa detta genom att visa att VL är en delmängd i HL och vice versa. Resonemanget ovan är i princip allt vi behöver.)

Vad är ordningen på denna grupp?

Hej! Ber om ursäkt att jag glömt svara på detta inlägg. Jag läste ditt svar, men svarade aldrig på det. Nu idag stötte jag på en uppgift i en annan kontext som bad mig svara på exakt samma fråga som denna tråd handlar om (fast med konkreta siffror istället). Jag löste den för att jag kom ihåg det fina svar jag fick här.

Tack! Jag är nöjd! Och jag tror aldrig att cykliska delgrupper hade klickat så bra om jag inte fick en så bra förklaring av dig!

Svara