Ortogonal projektion på plan + linjär avbildning
Här är en gammal tenta-uppgift: 
Och här kommer en bild på facit:

Jag vet hur man räknar ut en ortogonal projektion av en vektor på en annan vektor, men här tappar jag bort mig. Först och främst, vad är syftet med att konstruera en bas i R^3?
Om man skall projicera vektorn v på planet så kan man använda formeln
ProjPlan(v) = v - (v•n)n/|n|2, där n är en normalvektor till planet.
Vad de gör är istället att först bestämma projektionens matris D relativt en bas av egenvektorer till projektionen. Matrisen D får då en enkel diagonalform. Sedan transformerar de D med basbytesmatriser (likformighetstransformation) så att de får matrisen relativt standardbasen.
Tycker att lösningsförslaget är väldigt kortfattat och vagt. Basen som han skapar för R3 består av egenvektorer till avbildningen T. Minns du definitionen av egenvektorer? Sådana vektorer x så att T(x)= Ax = kx , med andra ord så är det vektorer som inte ändrar riktning vid linjär avbildning, i vårt fall är det de vektorer som inte ändrar riktning vid projektion på planet. Tänk dig att du har ett A4 papper som representerar planet, och en vektor (typ en penna) som pekar t.ex. 45* längs med planet, om du projicerar denna vektor på planet så får du då vektorns, eller pennans, skugga på planet som pekar i en annan riktning än den ursprungliga vektorn som var i 45* med planet. Om du däremot tar en vektor som redan är i planet och projicerar den på planet, så får du bara samma vektor. Typ om pennan ligger platt på planet, då är dess skugga lika med pennan själv och pekar i exakt samma riktning och har samma längd, alltså har projektionen (avbildningen) inte ändrat vektorns riktning och vektorn i planet är därför en egenvektor för just denna avbildning. Egenvärdet är k= 1. För en vektor som pekar rakt ut ur pappret ändras inte riktningen men längden ändras med en faktor 0, vilket är egenvärdet.
Okej så till din fråga, varför gör han då en bas av egenvektorer? Jo eftersom standardmatrisen för en linjär avbildning består av bilden av basvektorerna, och om basvektorerna är egenvektorerna så blir standardmatrisen väldigt enkel då bilden av basvektorn (egenvektorn) alltid kommer vara en skalär k gånger vektorn. Detta kan du se i matisen D, där bilden av första basvektorn v1 är (1,0,0) eftersom det ligger i planet och därmed ej ändras vid projektion, samma för v2, och för v3 som är en normal projiceras den på nollvektorn som är (0,0,0). Därför är D matrisen för avbildningen i basen av egenvektorer, som han sedan skriver om i standardbasen.
Ett annat sätt att göra detta utan att byta bas är att projicera basvektorerna i R3, alltså e1,e2,e3, på normalen av planet sedan subtrahera basvektorn med resultatet av denna projektion, se bild. 
hjalpmig123 skrev:Tycker att lösningsförslaget är väldigt kortfattat och vagt. Basen som han skapar för R3 består av egenvektorer till avbildningen T. Minns du definitionen av egenvektorer? Sådana vektorer x så att T(x)= Ax = kx , med andra ord så är det vektorer som inte ändrar riktning vid linjär avbildning, i vårt fall är det de vektorer som inte ändrar riktning vid projektion på planet. Tänk dig att du har ett A4 papper som representerar planet, och en vektor (typ en penna) som pekar t.ex. 45* längs med planet, om du projicerar denna vektor på planet så får du då vektorns, eller pennans, skugga på planet som pekar i en annan riktning än den ursprungliga vektorn som var i 45* med planet. Om du däremot tar en vektor som redan är i planet och projicerar den på planet, så får du bara samma vektor. Typ om pennan ligger platt på planet, då är dess skugga lika med pennan själv och pekar i exakt samma riktning och har samma längd, alltså har projektionen (avbildningen) inte ändrat vektorns riktning och vektorn i planet är därför en egenvektor för just denna avbildning. Egenvärdet är k= 1. För en vektor som pekar rakt ut ur pappret ändras inte riktningen men längden ändras med en faktor 0, vilket är egenvärdet.
Okej så till din fråga, varför gör han då en bas av egenvektorer? Jo eftersom standardmatrisen för en linjär avbildning består av bilden av basvektorerna, och om basvektorerna är egenvektorerna så blir standardmatrisen väldigt enkel då bilden av basvektorn (egenvektorn) alltid kommer vara en skalär k gånger vektorn. Detta kan du se i matisen D, där bilden av första basvektorn v1 är (1,0,0) eftersom det ligger i planet och därmed ej ändras vid projektion, samma för v2, och för v3 som är en normal projiceras den på nollvektorn som är (0,0,0). Därför är D matrisen för avbildningen i basen av egenvektorer, som han sedan skriver om i standardbasen.
Ett annat sätt att göra detta utan att byta bas är att projicera basvektorerna i R3, alltså e1,e2,e3, på normalen av planet sedan subtrahera basvektorn med resultatet av denna projektion, se bild.
Håller med om att lösningsförslaget är uselt, men det är tyvärr mer regel än undantag vad gäller tentor från KTH och LTH. När man fastnar på en fråga får man sitta och gissa och testa sig fram innan polletten trillar ned. Alternativt fråga här då.
Oavsett vilket, tack för hjälpen. Jag förstod mycket mer nu. Dock förstår jag inte hur man hittar D? Såhär i efterhand när jag ser matrisen D och även att du förklarar att v1 och v2 ligger i planet medan v3 inte gör det, så känns det väldigt naturligt. Men hade aldrig kommit dit på egen hand, så att säga. Jag antar att det även måste gå att räkna fram på något vis, utan att man måste kunna "se det".
PATENTERAMERA skrev:Om man skall projicera vektorn v på planet så kan man använda formeln
ProjPlan(v) = v - (v•n)n/|n|2, där n är en normalvektor till planet.
Vad de gör är istället att först bestämma projektionens matris D relativt en bas av egenvektorer till projektionen. Matrisen D får då en enkel diagonalform. Sedan transformerar de D med basbytesmatriser (likformighetstransformation) så att de får matrisen relativt standardbasen.
Vad är vektorn v i det här fallet?
Det är naturligtvis vektorn som du skall projicera på planet.
PATENTERAMERA skrev:Det är naturligtvis vektorn som du skall projicera på planet.
Och vad är den vektorn i det här fallet (i uppgiften ovan)? Den enda vektor jag kan utläsa direkt i uppgiften är normalvektorn (1,1,1) men man kanske kan räkna ut v på något smidigt sätt också?
Det är en variabel vektor som kan representera vilken vektor som helst. Precis som x representerar ett godtyckligt värde när man skriver f(x).
Just när man byter till egenvektorbas och du har ngn enklare avbildning typ en projektion på vektor, linje eller plan, så handlar det nog mest om känsla för egenvektorer. Anledningen till att man ens byter bas överhuvudtaget är för att göra livet enklare, diagonalmatrisen D är mycket trevligare att hantera än A = PDP^-1 och tar t.ex. mindre plats på en dator. Ett annat exempel, om du har en linjär avbildning som ger rotation kring Z-axeln i R3, vad blir egenvektorn då?
"Dock förstår jag inte hur man hittar D?" Matrisen för en linjär avbildning består alltid av bilden av basvektorerna, oavsett bas. När vi menar standardmatris menar vi ju matrisen föra avbildningen i vår standard bas {e1,e2,e3}. Här är standardmatrisen
men i en annan bas, säg egenbasen V = {v1,v2,v3} så blir matrisen
T(v1) = v1, T(v2) = v2, T(v3) = 0
Och eftersom vi är i egenbasen är v1 = (1,0,0) v2 = (0,1,0). Detta kanske är lite svårt att förstå men det är ju för att vi är i en ny bas med ett annorlunda koordinatsystem. I vårt standard kartesiska koordinatsystem har vi ju att om vi t.ex. rört oss längs hela vektorn e1 har vi kommit till punkten 1 på x-axeln. Nu i egenvektor-koordinatsystemet, om vi rör oss längs hela vektorn v1 från botten till tippen så har vi kommit till punkten 1 längs med v1-axeln. Jag tror att man kan tänka så, det är så jag har gjort iaf. Har skissat hur basvektorerna ser ut i egenvektorbasen i Geogebra:
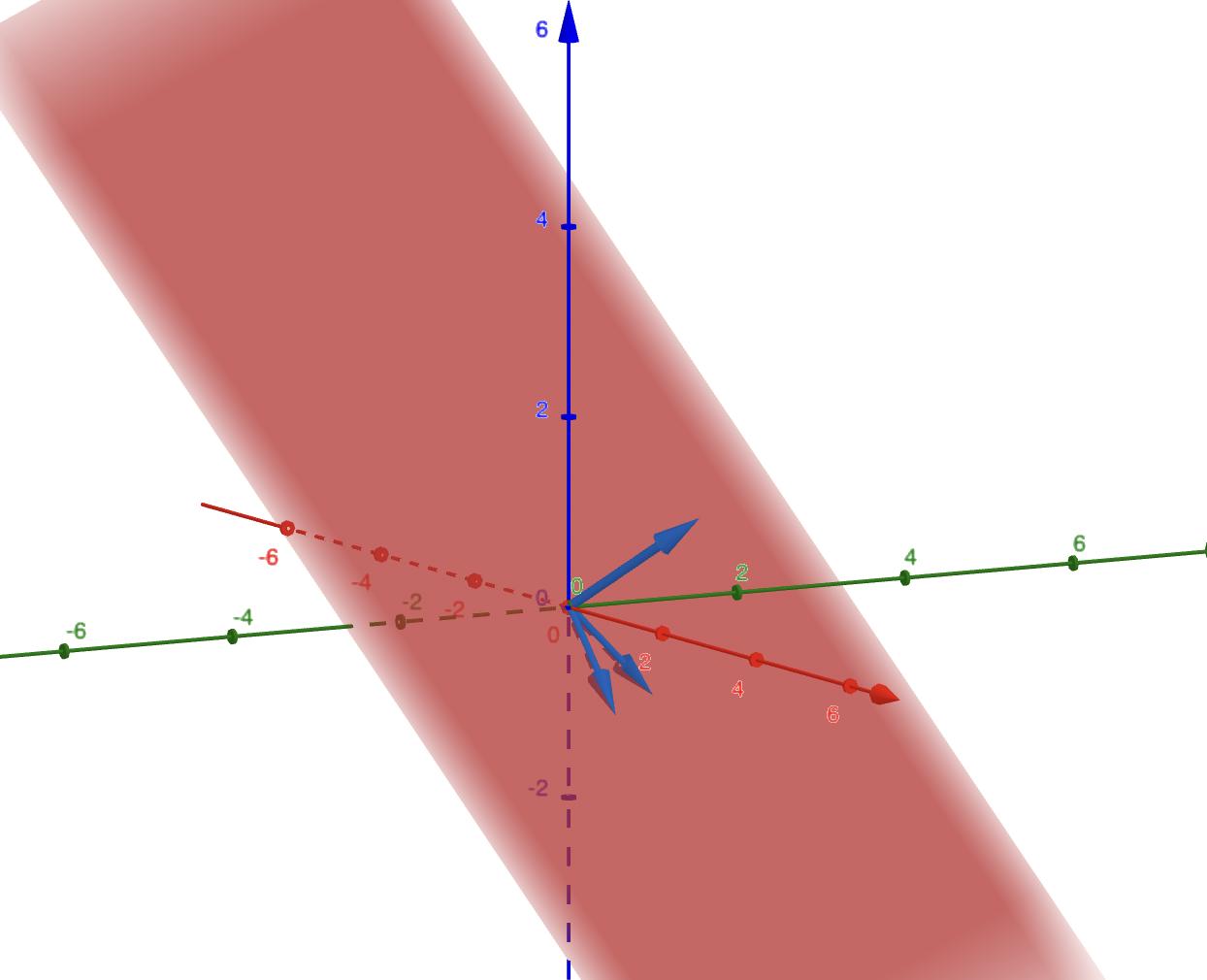

I första bilden ser du planet och de blåa vektorerna som är v1,v2,v3 i standardbasen. I sista bilden ser du basvektorerna {v1,v2,v3} för sig själva som nu utgör ett nytt koordinatsystem i egenbasen. Om vi befinner oss på tippen av v3 (den som är vinkelrät mot båda) så är vi i punkten (0,0,1).
Rekommenderar 3blue1browns video om egenvektorer, den hjälpte mig rätt mkt.

