Överljudsflygplan
Hur ska jag tänka här?
Då jag inte har några värden så ser jag inte hur jag kan gör en uträkning med formeln:
u/v = 1/sin (alfa)
Jag vet att det blir en "svallvåg" när flygplanet har en högre hastighet än ljudets hastighet. Men mer än så har jag inte förstått ännu, tycker att informationen i Heureka är bristfälling gällande chockvågor.

Hej Mattelinnea!
Överljudsflygplanets hastighet kan inte beräknas exakt i denna uppgift utan kan endast approximeras med hjälp av grafisk avläsning.
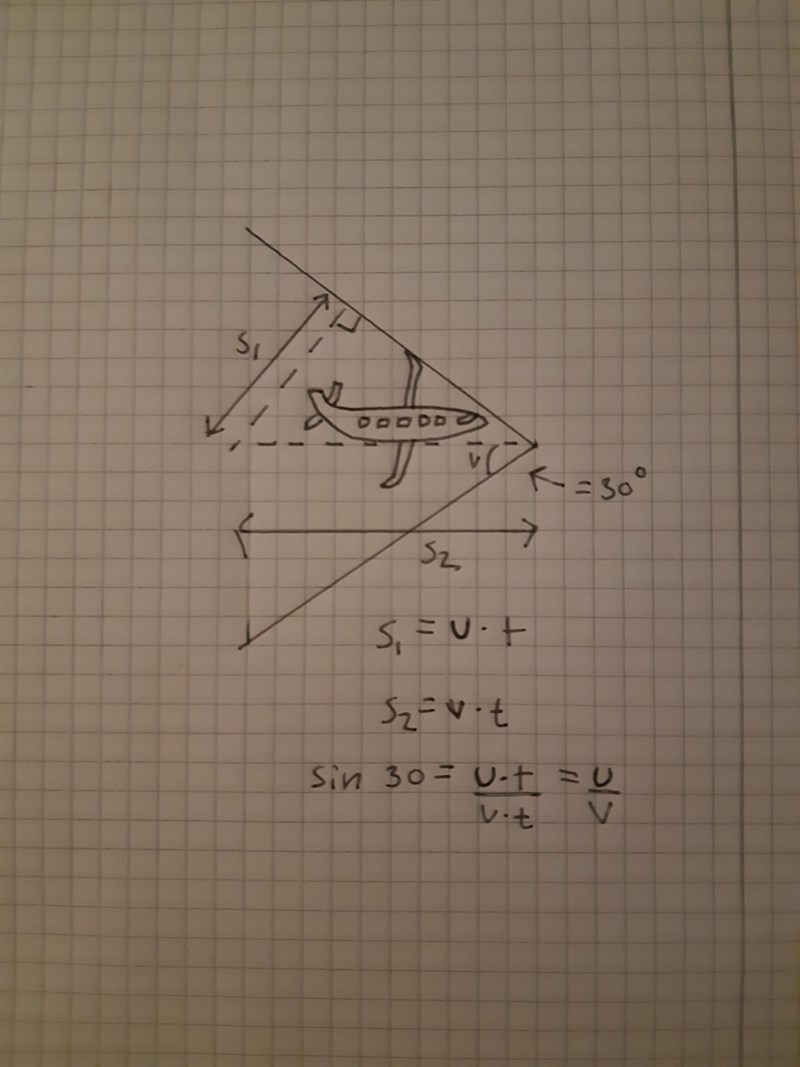
Vinkeln vid flygplanet, innanför strecken, får jag till 60 grader med hjälp av gradskiva. Denna vinkel måste man först dela på två genom att dra en horisontell linje mellan linjerna (ljudvågorna) vid flygplanet innan man kan använda vinkeln i trigonometriska beräkningar.
Ekvationen u/v = sin (a) blir => u/v = sin (30°) = 1/2. Det betyder att flygplanet har hunnit färdats dubbelt så lång sträcka än ljudet inom samma tidsperiod. Eftersom v måste bara dubbelt så stort än u för att u/v ska bli 1/2.
Därför blir svaret Ca två gånger ljudets hastighet.
Extra kommentar: Om flygplanet skulle åka i precis ljudets hastighet, hade man fått en figur där ljudvågornas linjer går ut vinkelrätt från flygplanet och deras totala vinkel blir 180 grader. 180/2 = 90 grader. u/v = sin (90) = 1, vilket ger att u och v har samma längd. Ju snabbare flygplanet åker, desto snävare vinkel.
Hoppas det här var till någon hjälp :)
Truppeduppe skrev:Hej Mattelinnea!
Överljudsflygplanets hastighet kan inte beräknas exakt i denna uppgift utan kan endast approximeras med hjälp av grafisk avläsning.
Vinkeln vid flygplanet, innanför strecken, får jag till 60 grader med hjälp av gradskiva. Denna vinkel måste man först dela på två genom att dra en horisontell linje mellan linjerna (ljudvågorna) vid flygplanet innan man kan använda vinkeln i trigonometriska beräkningar.
Ekvationen u/v = sin (a) blir => u/v = sin (30°) = 1/2. Det betyder att flygplanet har hunnit färdats dubbelt så lång sträcka än ljudet inom samma tidsperiod. Eftersom v måste bara dubbelt så stort än u för att u/v ska bli 1/2.
Därför blir svaret Ca två gånger ljudets hastighet.
Extra kommentar: Om flygplanet skulle åka i precis ljudets hastighet, hade man fått en figur där ljudvågornas linjer går ut vinkelrätt från flygplanet och deras totala vinkel blir 180 grader. 180/2 = 90 grader. u/v = sin (90) = 1, vilket ger att u och v har samma längd. Ju snabbare flygplanet åker, desto snävare vinkel.
Hoppas det här var till någon hjälp :)
Tack så jätte jätte mycket!!
Du förklarade väldigt bra och genomgående så nu förstår jag precis!
Har delat ditt svar med klasskamraterna och vi är alla väldigt tacksamma för att du lade ner tid på en lördag för att hjälpa! :)

