Parallelltransversal och likformighet
Jag behöver hjälp med att lösa denna uppgift. Jag är med på att jag ska använda Pythagoras sats för att få fram sidan AC efter jag räknat ut hela höjden med hjälp av likformighet men är lite osäker på hur jag ska använda skalan.
Triangeln ABC är likbent. Basen AB är 17,4mm. En parallelltransversal DE delar triangelns lika långa sidor i förhållandet 5:3 (AD:DC). Höjden i topptriangeln är 11,6 mm. Bestäm sidan AC.
Mam behöver nog rita för att hålla ordning på allting. Vill du rita och ladda upp?
Såhär fick jag till det, jag har inte ritat enligt någon skala utan bara skrivit dit längderna som anges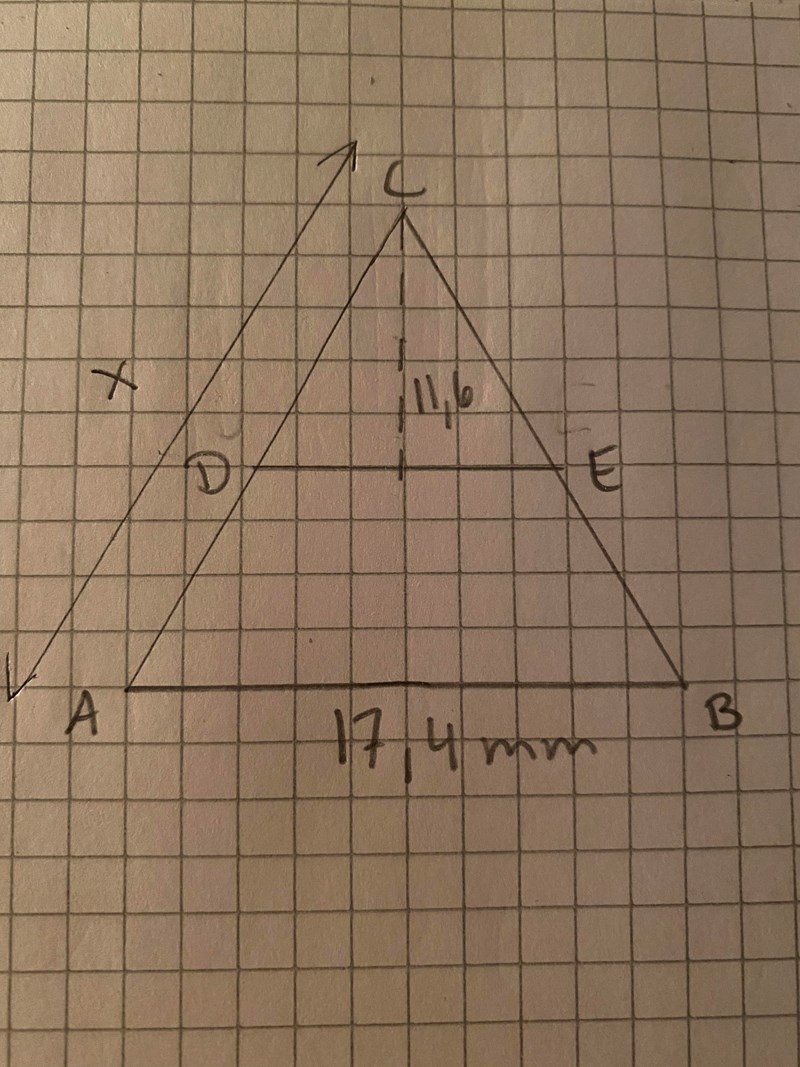
Förhållandet 5:3 betyder att AD/DC = 5/3. Om vi kallar mittpunkten på DE för G och mittpunkten på AB för H, så betyder det att HG/GC också är 5/3. Kan du räkna ut HC då?
Hur ska jag räkna med 5:3? Hur ska jag ställa upp det?
Någon som kan ge mig en ledtråd på hur man ställer upp? Alltså skalenligt 5:3?
Jag testade och fick fram att 5/3≈1,66. Sedan tog jag 1,66*11,6 och fick svaret 19,256. Kan detta vara längden på HC? Om detta är rätt är det bara att använda Pythagoras sats för att räkna ut längden AC?
Du har räknat ut längden på HG.
Ok, då adderar jag 11,6 till 19,256 och använder sedan Pythagoras sats


