Parallelepiped, vektorgeometri
Hej, skulle man kunna få en gnutta hjälp tack. 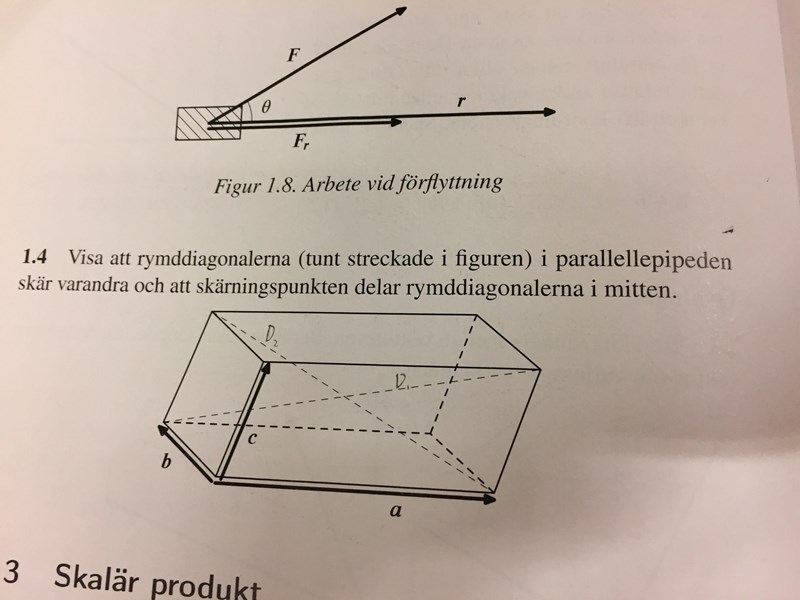 Jag har kommit fram till att
Jag har kommit fram till att
Jag har sett i en tidigare uppgift att man ska göra på detta viset, definera de båda som vektorer och sedan på något magiskt sätt använda och för att visa att de skär varandra. Jag skulle även kunna lista ut vad definitionen för vektorn som har slutpunkt vid skärningspunkten men jag vet inte riktigt hur jag kan "VISA" att de skär varandra med hjälp av det. Någon som kan förklara hur man "visar" och hur det funkar. Tack.
EDIT: Kan tillägga att facits svar är: Utifrån hörnen där vektorerna har sina startpunkter är vägen till mitten av diagonalerna respektive
Egen kommentar: Jag förstår att vägen till mitten av diagonalvektorerna kan skrivas på de sättet, det skulle också kunna skrivas Men det klarnar ändå inte till i huvudet. Hur kan detta visa att två stycken rymddiagonaler skär varandra?
Det kan vara svårt att tänka vektorer i tre dimensioner.
Tänk dig då (titta samtidigt i figuren) två vektor-summeringar i två dimensioner och summera sedan dessa.
Affe Jkpg skrev:Det kan vara svårt att tänka vektorer i tre dimensioner.
Tänk dig då (titta samtidigt i figuren) två vektor-summeringar i två dimensioner och summera sedan dessa.
Jag har ritat lite efter att ha läst din kommentar.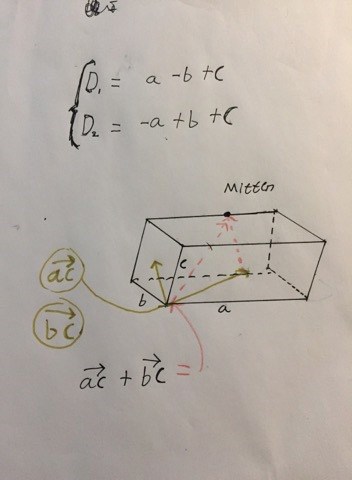
Både och har sin slutpunkt på utsidan av parallellepipeden alltså typ på utsidan av väggarna.. Du förstår nog vad jag menar. De är tvådimensionella.
Om man lägger ihop dem så får man en vektor som nuddar mitten av taket intill väggen. Är det korrekt så som jag har ritat den röda vektorn ?
Om jag nu gjort rätt så förstår jag fortfarande inte hur detta kan "bevisa" att diagonalerna skär varandra i mitten.
Om du inte lägger till startpunkten för vardera vektorn, så är det svårt att visa att de skär varandra. Den ena linjen startar i punkten (0,b,0)och "rör sig" i riktnigen , den andra startar i punkten (a,0,0) och "rör sig" i riktningen . Den första linjen kan alltså skrivas som (x,y,z) = (0,b,0)+k(a-b+c) där och liknande för den andra linjen. Gör en ekvation av detta och lös ut k.
Korra skrev:Affe Jkpg skrev:Det kan vara svårt att tänka vektorer i tre dimensioner.
Tänk dig då (titta samtidigt i figuren) två vektor-summeringar i två dimensioner och summera sedan dessa.Jag har ritat lite efter att ha läst din kommentar.
Både och har sin slutpunkt på utsidan av parallellepipeden alltså typ på utsidan av väggarna.. Du förstår nog vad jag menar. De är tvådimensionella.
Om man lägger ihop dem så får man en vektor som nuddar mitten av taket intill väggen. Är det korrekt så som jag har ritat den röda vektorn ?
Om jag nu gjort rätt så förstår jag fortfarande inte hur detta kan "bevisa" att diagonalerna skär varandra i mitten.
Nä...just dä
Den ena helgröna vektor-pilen har du ritat korrekt. Sedan får man:
Affe Jkpg skrev:
Nä...just dä
Den ena helgröna vektor-pilen har du ritat korrekt. Sedan får man:
Jag kan föreställa mig hur ser ut. Då följer man vektor b och sedan så följer man halvvägs och då kommer man till diagonalernas skärningspunkt. Man kan göra liknande med den andra diagonalen också. Detta är ju facits svar, mitt problem är bara att jag inte förstår hur detta på något sätt visar att de två diagonalerna "SKÄR" varandra. :) Så hur ska man tänka egentligen för att förstå det?
Korra skrev:Affe Jkpg skrev:Nä...just dä
Den ena helgröna vektor-pilen har du ritat korrekt. Sedan får man:
Jag kan föreställa mig hur ser ut. Då följer man vektor b och sedan så följer man halvvägs och då kommer man till diagonalernas skärningspunkt. Man kan göra liknande med den andra diagonalen också. Detta är ju facits svar, mitt problem är bara att jag inte förstår hur detta på något sätt visar att de två diagonalerna "SKÄR" varandra. :) Så hur ska man tänka egentligen för att förstå det?
Fortsätt med vektor-beräkningen vid punkterna ....
Affe Jkpg skrev:Korra skrev:Affe Jkpg skrev:Nä...just dä
Den ena helgröna vektor-pilen har du ritat korrekt. Sedan får man:
Jag kan föreställa mig hur ser ut. Då följer man vektor b och sedan så följer man halvvägs och då kommer man till diagonalernas skärningspunkt. Man kan göra liknande med den andra diagonalen också. Detta är ju facits svar, mitt problem är bara att jag inte förstår hur detta på något sätt visar att de två diagonalerna "SKÄR" varandra. :) Så hur ska man tänka egentligen för att förstå det?
Fortsätt med vektor-beräkningen vid punkterna ....
Förlåt, nu är jag inte riktigt med längre.
då får jag den guldfärgade (inte gröna! :p) vektorn precis som jag har ritat.
Om jag nu ska addera den vektorn med en annan vektor då utgår man från slutpunkten av och ba lägger till vektor Nu har jag hamnat i hörnet på en höjd av c/2. Right?
Jämför nu med ditt ursprungliga uttryck för
Affe Jkpg skrev:Jämför nu med ditt ursprungliga uttryck för
Haha ja det stämmer ju, får fram det jag fick fram från början på d1 :P Det känns som att du förväntar dig att jag ska förstå hur allt har gått till nu men det gör jag inte. Vill du höra vilken det av allt det vi gjorde jag inte förstod?
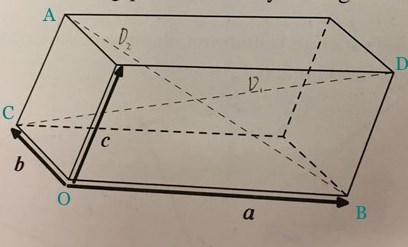
Jag väljer att lägga origo (0) enligt bilden.
Om vi ställer oss i origo och går till C (genom att gå vektor b)och sedan halva diagonalen ska vi hamna i samma punkt som när vi ställer oss i origo går c uppåt, b åt vänster (nu är vi i punkten A) och slutligen halva diagonalen .
Guggle skrev:
Jag väljer att lägga origo (0) enligt bilden.
Om vi ställer oss i origo och går till C (genom att gå vektor b)och sedan halva diagonalen ska vi hamna i samma punkt som när vi ställer oss i origo går c uppåt, b åt vänster (nu är vi i punkten A) och slutligen halva diagonalen .
Jag förstår exakt vad du menar och jaa om vi tar den första vägen eller den andra så ska vi hamna på samma plats. Finns det något sätt att kontrollera att vi har hamnat på samma plats?
Korra skrev:Jag förstår exakt vad du menar och jaa om vi tar den första vägen eller den andra så ska vi hamna på samma plats. Finns det något sätt att kontrollera att vi har hamnat på samma plats?
Ja. Uttryck först diagonalerna i vektorerna a, b och c
Diagonalen
A och B kan du uttrycka i vektorerna a, b och c.
Gör på samma sätt med den andra diagonalen.
Slutligen går du de två vägarna beskrivna ovan och ser att du får exakt samma uttryck, du når alltså samma lägesvektor vilken väg du än väljer => punkterna sammanfaller = linjerna korsas.
(En läges- eller ortsvektor är en vektor från origo till en punkt i rummet.)
Korra skrev:Affe Jkpg skrev:Jämför nu med ditt ursprungliga uttryck för
Haha ja det stämmer ju, får fram det jag fick fram från början på d1 :P Det känns som att du förväntar dig att jag ska förstå hur allt har gått till nu men det gör jag inte. Vill du höra vilken det av allt det vi gjorde jag inte förstod?
Visst vill jag veta .... vad det va du inte förstod :-)
Som Guggle sedan skriver så är parallell-epipeden symetrisk. Analys av ska bli ........
Guggle skrev:Korra skrev:Jag förstår exakt vad du menar och jaa om vi tar den första vägen eller den andra så ska vi hamna på samma plats. Finns det något sätt att kontrollera att vi har hamnat på samma plats?
Ja. Uttryck först diagonalerna i vektorerna a, b och c
Diagonalen
A och B kan du uttrycka i vektorerna a, b och c.
Gör på samma sätt med den andra diagonalen.
Slutligen går du de två vägarna beskrivna ovan och ser att du får exakt samma uttryck, du når alltså samma lägesvektor vilken väg du än väljer => punkterna sammanfaller = linjerna korsas.
(En läges- eller ortsvektor är en vektor från origo till en punkt i rummet.)
Jag förstår när du skriver Diagonalen Nu ska jag följa din instruktion och göra samma sak på den andra diagonalen.
"Slutligen går du de två vägarna beskrivna ovan och ser att du får exakt samma uttryck, du når alltså samma lägesvektor vilken väg du än väljer => punkterna sammanfaller = linjerna korsas."
Den delen är jag inte riktigt med på. Om jag går och sedan Hur får jag exakt samma uttryck?
Korra skrev:Guggle skrev:
Jag förstår när du skriver Diagonalen Nu ska jag följa din instruktion och göra samma sak på den andra diagonalen.
Bra!
Den ena vägen är:
Du ställer dig i origo. Gå b åt vänster (vi är nu i C), gå c uppåt (vi är nu i A), gå halva .
Sammanlagt blir alltså den vägen
Gör samma sak för den andra vägen, dvs ställ dig i origo, gå till punkten C (vilken vektor blir det?) och sedan halva . Hamnar du i samma punkt?
Vad säger det om rymddiagonalerna?
Guggle skrev:Korra skrev:Guggle skrev:Jag förstår när du skriver Diagonalen Nu ska jag följa din instruktion och göra samma sak på den andra diagonalen.
Bra!
Den ena vägen är:
Du ställer dig i origo. Gå b åt vänster (vi är nu i C), gå c uppåt (vi är nu i A), gå halva .
Sammanlagt blir alltså den vägen
Gör samma sak för den andra vägen, dvs ställ dig i origo, gå till punkten C (vilken vektor blir det?) och sedan halva . Hamnar du i samma punkt?
Vad säger det om rymddiagonalerna?
Om jag går från O till skärningspunkten via den vägen du beskrev så är det samma sak som att bara dra en vektor från O till skärningspunkten alltså om vi kallar skärningspunkten för X så ger
Jag är väldigt förvirrad nu. Jag gör såhär, jag börjar om på nytt och jag ska visa exakt hur jag gör. Men om jag har förstått din poäng nu så vill du att jag ska definiera de båda diagonalerna och sedan så ska jag med hjälp av dessa diagonaler beskriva två olika ortsvektorer som har sin slutpunkt i mitten. (Jag gör bara detta för att när jag ser på d1 och d2 så minns jag inte längre hur och varför de är lika med kombinationen av de andra vektorerna.)
Steg 1: Definiera och
Vi kallar skärningspunkten för X Nu ska jag utnyttja för att ta mig dit.
Och nu ska jag utnyttja för att ta mig dit.
Hmm intressant :D Om jag har gjort rätt nu så har jag förstått vägen hit 100% nu är det den sista lilla biten. "Vad säger det om rymddiagonalerna?" Jaa du... Jag har nu skapat 2 vektorer som är likadana genom att ta två olika vägar till X via de båda diagonalerna. Hmm Kan du förklara vad det säger om rymddiagonalerna? Jag kan inte komma på det är jag rädd. :)
Korra skrev:
Steg 1: Definiera och
Vi kallar skärningspunkten för X Nu ska jag utnyttja för att ta mig dit.
Och nu ska jag utnyttja för att ta mig dit.
Ja, fast från början vet du inte om punkterna sammanfaller. Det du har gjort är att först ställa dig i A, gå halva sträckan från A till B (dvs halva rymddiagonalen och så har du hamnat i en punkt P1. Sedan har du ställt dig i C och gått halvvägs från C till D (dvs halva rymddiagonalen ) och hamnat i en punkt P2. Du upptäcker nu att dessa båda punkter är en och samma punkt. P1=P2
Det kan bara inträffa om rymddiagonalerna skär varandra och skärningspunkten delar de båda rymddiagonalerna i mitten.
Guggle skrev:Korra skrevDet kan bara inträffa om rymddiagonalerna skär varandra och skärningspunkten delar de båda rymddiagonalerna i mitten.
varför kan de bara inträffa då?
Korra skrev:Guggle skrev:Korra skrevDet kan bara inträffa om rymddiagonalerna skär varandra och skärningspunkten delar de båda rymddiagonalerna i mitten.
varför kan de bara inträffa då?
Eftersom P1 ligger på och P2 ligger på och vi har hamnat i en och samma punkt måste diagonalerna korsas någonstans.
Dessutom har vi gått halva diagonalernas längder, alltså är vi exakt mitt på varje diagonal när de möter varandra.
Mötespunkten vi hittat ligger exakt mitt i parallellepipeden. För att gå till mötespunkten går vi 1/2 av varje sida,
Vilket vi hade kunnat räkna ut med symmetrianalys :)
Guggle skrev:Korra skrev:Guggle skrev:Korra skrevDet kan bara inträffa om rymddiagonalerna skär varandra och skärningspunkten delar de båda rymddiagonalerna i mitten.
varför kan de bara inträffa då?
Eftersom P1 ligger på och P2 ligger på och vi har hamnat i en och samma punkt måste diagonalerna korsas någonstans.
Dessutom har vi gått halva diagonalernas längder, alltså är vi exakt mitt på varje diagonal när de möter varandra.
Mötespunkten vi hittat ligger exakt mitt i parallellepipeden. För att gå till mötespunkten går vi 1/2 av varje sida,
Vilket vi hade kunnat räkna ut med symmetrianalys :)
Okej, jag nöjer mig med den kunskapen som jag har fått. Tack så jättemycket för hjälpen, du är jätteduktig på att förklara och väldigt vänlig.
:)





