Parametrisering
Hej allihopa :)
Jag undrar en sak om parametrisering. Vi har gjort denna uppgift i klassen:
Visa spoiler
Oh nice! En spoilerfunktion!!
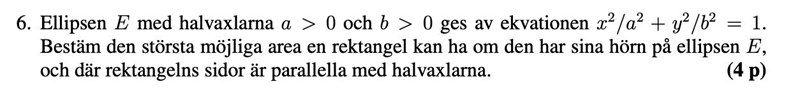
För att räkna uppgiften vi fick dela den i 4 rektanglar och parametrisera ellipsen med:
Jag undrar nu varför är det inte , eftersom vi ska parametrisera på en fjärdedel av intervallet? Det kändes logisk förut men nu tvekar jag.
Viktigare:
Hur parametriserar man paraboles och hyperboles med trigonometriska uttryck?
Visa spoiler
Bra jobbat med spoiler funktion Pluggakuten!
Det är t eftersom vi endast parametriserar en fjärdedel av cirkeln. Om vi skriver 4t får vi hela cirkeln.
En hyperbol parametriseras med formeln . En parabel parametriseras genom att sätta x eller y till t, och uttrycka den andra variabeln i t. Exempelvis . Sätt x = t, och y blir då lika med t3.
Hur skulle det se ut om vi parametriserade på hela cirkeln och jobbade på Area1?
Vad är h i din hyperbole parametrisering?
Det går väl egentligen lika bra. I ursprungsuppgiften räknar vi med , så det går nog bra det med.
Ursäkta, formeleditorn vet tydligen inte vad cosh(x) och sinh(x) är för något. Det är hyperbolicusfunktionerna. :)
dajamanté skrev:Hur skulle det se ut om vi parametriserade på hela cirkeln och jobbade på Area1?
Vad är h i din hyperbole parametrisering?
Om du vill parametrisera hela ellipsen behöver du helt enkelt bara ändra så att . är ju vinkeln mellan x-axeln och sträckan från origo till punkten på ellipsen. Om vi vill ta ett helt varv skall vi då låta vinkeln vara mellan och (ett helt varv).

Tänk det som att punkten promenerar runt ellipsen beroende på vinkeln . Om vi låter vinkeln variera mellan och kommer vi att promenera runt hela ellipsen. Om du sätter siffror inuti sinus- och cosinusfunktionen, t.ex. kommer punkten att promenera snabbare. Då behöver vi bara låta gå mellan och för att täcka hela ellipsen. Man gör inte detta så ofta eftersom det försvårar förståelsen ( blir ju inte längre ett varv, utan fyra).
Det blev lite pannkaka med formateringen i Smutstvätts inlägg. Vad som menas är de hyperboliska trigfunktionerna (du vet de där du höll på med när du skulle lösa integraler). De parametriserar nämligen en halv hyperbel (det är därför de heter hyperboliska trigfuntkioner):

Här låter vi vara alla reella tal (eftersom parabeln har en oändlig kurvlängd, till skillnad från en ellips). Observera att det inte heller finns någon enkel koppling till en vinkel med parablerna.
För att få den andra halvan av hyperbeln kan vi lägga till minustecken i parametriseringen:

Tack till båda. Jag är ungefärligt med.
På en ungefärligt nivå.




