parametrisering av kurva (flervariabelanalys)
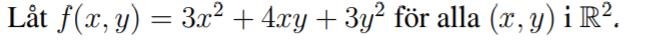
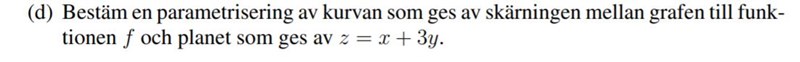
har fastnat på denna
I andra fall brukar jag ställa upp ett ekvationssystem men i detta fall har jag ju bara en ekvation nämligen den som står i d) uppgiften, själva funktionen f är ju ingen ekvation
Hur går man till väga då? eller har jag tolkat uppgiften fel?
z = x+3y är väl en ekvation?
Edit: ja, det sade du själv. Men z =f(x, y) är ju också en.
Som laguna är inne på definierar vi konstigt nog grafen av en reellvärd funktion som punktmängden
I de flesta kurser.
okej tack då är jag med på det
vet dock inte hur jag går vidare ändå, finns det något uppenbart jag ska byta ut x och y till eller hur prövar man sig fram? vad är nästa steg?
sätter jag x = t hjälper det inte mig så mycket . eller ska jag byta till polära koordinater?
Så definitionen av en graf är alltså
Du vet också att
Vad får du om du sätter dem lika?
Ställ sedan upp en parameterframställning
Jroth skrev:Så definitionen av en graf är alltså
Du vet också att
Vad får du om du sätter dem lika?
Ställ sedan upp en parameterframställning
jag får
men om jag löser ut x eller y hur denna blir det ett långt uttryck, känns inte som att det är rätt väg när jag gör så
Ekvationen beskriver en ellips i xy-planet. Tyvärr ligger ellipsen inte i origo. Det finns lite olika strategier att hantera den.
En vacker strategi är att införa ett kartesiskt system som med två av de ortogonala basvektorerna i planet , din parameterframställning av skärningslinjen kommer ju ligga i detta plan.
Jroth skrev:Ekvationen beskriver en ellips i xy-planet. Tyvärr ligger ellipsen inte i origo. Det finns lite olika strategier att hantera den.
En vacker strategi är att införa ett kartesiskt system som med två av de ortogonala basvektorerna i planet , din parameterframställning av skärningslinjen kommer ju ligga i detta plan.
jag har precis börjat med denna kurs så har inte "lärt" mig några strategier än eller hunnit lösa så långa uppgifter
hur går man tillväga med denna strategi som du beskriver?
Om du precis har börjat med kursen är det nog lite överkurs att bestämma koordinater och halvaxlar för ellipsen.
I början av tråden nämnde du polära koordinater. Låt oss nöja oss med att ställa upp ekvationen i polära koordinater, låt
Vad blir uttrycket då? (Använd trigonometriska ettan för att förenkla)
dela båda sidor med
Lös ut
En parameterframställning ges nu av
Jroth skrev:Om du precis har börjat med kursen är det nog lite överkurs att bestämma koordinater och halvaxlar för ellipsen.
I början av tråden nämnde du polära koordinater. Låt oss nöja oss med att ställa upp ekvationen i polära koordinater, låt
Vad blir uttrycket då?
dela båda sidor med
Lös ut
En parameterframställning ges nu av
okej jag ska testa med det, och återkommer
men hur vet man att man ska ta polära koordinater? jag nämnde det för jag hörde någon säga något om det i ett klipp
men är det något standard man alltid testar med eller gör man det mest när det gäller cirklar / ellipser?
men hur vet man att man ska ta polära koordinater? jag nämnde det för jag hörde någon säga något om det i ett klipp
men är det något standard man alltid testar med eller gör man det mest när det gäller cirklar / ellipser?
Det är en ganska vanlig metod även när det t ex handlar om "avståndet till origo" eller något liknande. Det är ju "en cirkel i förklädnad" eftersom alla punkter som ligger på ett visst avstånd från origo ligger på en cirkel.
Smaragdalena skrev:men hur vet man att man ska ta polära koordinater? jag nämnde det för jag hörde någon säga något om det i ett klipp
men är det något standard man alltid testar med eller gör man det mest när det gäller cirklar / ellipser?
Det är en ganska vanlig metod även när det t ex handlar om "avståndet till origo" eller något liknande. Det är ju "en cirkel i förklädnad" eftersom alla punkter som ligger på ett visst avstånd från origo ligger på en cirkel.
okej tack för hjälpen!
Jroth skrev:Om du precis har börjat med kursen är det nog lite överkurs att bestämma koordinater och halvaxlar för ellipsen.
I början av tråden nämnde du polära koordinater. Låt oss nöja oss med att ställa upp ekvationen i polära koordinater, låt
Vad blir uttrycket då? (Använd trigonometriska ettan för att förenkla)
dela båda sidor med
Lös ut
En parameterframställning ges nu av
okej jag har ändrat till polära koordinater och förenklat hela uttrycket och satt r på en sida och fått:
då har jag x(t) = rcost, y(t) = sint och z(t) får jag från z=x+3y = rcost + 3rsint
så r(t) = rcost , rsint , rcost + 3rsint
men vad har detta att göra med r som jag fick när jag förenklade och uttryckte i r(t) ? den använder vi ju inte ens
EDIT: Nu tror jag att jag börjar förstå
r motsvarar det uttrycket som vi löste fram genom ekvationssystemet
så det vi har gjort här är alltså att vi har två kurvor och skärningen mellan dessa kurvor motsvarar alltså en tredje kurva som vi har parametriserat fram? och den skärningen är alltså r(t) ? stämmer min teori?
Ja, det är nästan korrekt. Det vi gjort är att vi studerat skärningen mellan två ytor, och . Det ger oss ett samband mellan vinkeln och radien i xy-planet.
Sedan vet vi att ortsvektorn ges av
Så den fullständiga parameterframställningen för ditt uttryck är (och nu utnyttjar jag att
Om du vill göra den mer avancerade lösningsgången som jag förslog från början kommer du efter efter egenvärdesanalys inse att koordinatbytet
Ger dig en ellips som ser ut så här i uv-planet
Denna ellips har centrum och halvaxlarna och
Det ger dig småningom en korrekt parameterframställning som är ekvivalent med den du tagit fram.
Jroth skrev:Ja, det är nästan korrekt. Det vi gjort är att vi studerat skärningen mellan två ytor, och .
Så den fullständiga parameterframställningen för ditt uttryck är (och nu utnyttjar jag att
Om du vill göra den mer avancerade lösningsgången som jag förslog från början kommer du småningom inse att koordinatbytet
Ger dig en ellips som ser ut så här
Denna ellips har centrum och halvaxlarna och
Det ger dig småningom en korrekt parameterframställning som är ekvivalent med den du tagit fram.
okej okej skönt att jag äntligen hängde med, tack!
men vilken av metoderna är att föredra eller finns det inget sådant?
största skillnaden jag ser är att i den mer avancerade lösningen så ser man att det är en ellips direkt men inte i min (eller jag gör det inte iaf)
hur kommer man fram till det mer avancerade sättet? känner att det kan vara bra att kunna båda. Då ska jag göra ett variabelbyte eller vadå?
Notera att jag infört några rättelser i mitt tidigare inlägg, det råkade komma med 1/2 på variabelbytet som inte ska vara där.
Maremare skrev:
men vilken av metoderna är att föredra eller finns det inget sådant?
hur kommer man fram till det mer avancerade sättet? känner att det kan vara bra att kunna båda. Då ska jag göra ett variabelbyte eller vadå?
Det svåra är hitta ett variabelbyte som förenklar ellipsen (dvs vrider den rätt), det kan man t.ex. göra med metoder från fortsättningskursen i linjär algebra.
Det oftast möjligt att bara "gissa" sig fram till ett variabelbyte eftersom det i särklass vanligaste variabelbytet man använder i grundkurser är det jag visar ovan, vilket gör det till en bra gissning.
Du kommer få ett mycket krångligare uttryck om du löser det på det sätt man kanske kan misstänka att uppgiftsskaparen tänkt sig. Det går naturligtvis att visa att uttrycken är ekvivalenta (ger samma kurva).
Jroth skrev:Notera att jag infört några rättelser i mitt tidigare inlägg, det råkade komma med 1/2 på variabelbytet som inte ska vara där.
Maremare skrev:
men vilken av metoderna är att föredra eller finns det inget sådant?
hur kommer man fram till det mer avancerade sättet? känner att det kan vara bra att kunna båda. Då ska jag göra ett variabelbyte eller vadå?
Det svåra är hitta ett variabelbyte som förenklar ellipsen (dvs vrider den rätt), det kan man t.ex. göra med metoder från fortsättningskursen i linjär algebra.
Det oftast möjligt att bara "gissa" sig fram till ett variabelbyte eftersom det i särklass vanligaste variabelbytet man använder i grundkurser är det jag visar ovan, vilket gör det till en bra gissning.
Du kommer få ett mycket krångligare uttryck om du löser det på det sätt man kanske kan misstänka att uppgiftsskaparen tänkt sig. Det går naturligtvis att visa att uttrycken är ekvivalenta (ger samma kurva).
okej då är jag med, tusen tack för hjälpen!
Jroth skrev:Ja, det är nästan korrekt. Det vi gjort är att vi studerat skärningen mellan två ytor, och . Det ger oss ett samband mellan vinkeln och radien i xy-planet.
Sedan vet vi att ortsvektorn ges av
Så den fullständiga parameterframställningen för ditt uttryck är (och nu utnyttjar jag att
Om du vill göra den mer avancerade lösningsgången som jag förslog från början kommer du efter efter egenvärdesanalys inse att koordinatbytet
Ger dig en ellips som ser ut så här i uv-planet
Denna ellips har centrum och halvaxlarna och
Det ger dig småningom en korrekt parameterframställning som är ekvivalent med den du tagit fram.
jag har lyckats göra på det andra sättet
men får inte samma siffror som du
efter att jag satt ekvationerna lika och flyttar över allt till VL får jag
och ska jag få 1 i HL så multiplicerar jag med 5/9 i bägge led men då får jag
men du får omvänd plats på 25 och 9 ?
EDIT: såg fel det är samma, ska fortsätta å återkomma tack!
EDIT2: hur får man sen fram i parametriserings form? alltså u(t) v(t) etc?
EDIT3: jag tror jag löste det, gör jag såhär för u(t)
För om det är så då kan jag lösa de andra också, eller är det något tokigt?




