Partialintegration

Jag försöker lösa $\int_{1}^{2} \frac{x \ln x}{(1 + x}$ ²)2 genom partialintegration, men det känns som att det blir oändligt långa beräkningar. Vad gör jag för fel?

$\int f (x) g (x) = F (x) g (x) - \int F (x) g ´ (x)$

$f (x) = \frac{x}{(1 + x}$ ²)2 --> $F (x) = \frac{- 1}{2 (1 + x^{2})}$

$g (x) = \ln x$ --> $g' (x) = \frac{1}{x}$

$\frac{- 1}{2 (1 + x^{2})} \times \ln x - \int \frac{- 1}{2 x (1 + x^{2})}$

Problemet är nu att lösa ut $\int \frac{- 1}{2 x (1 + x^{2})}$ ...

Jag skulle föreslå partialbråksansats, där jag ansätter

$\dfrac{1}{x(1+x^2)}=\dfrac{A}{x}+\dfrac{Bx+C}{1+x^2}$ ,

som landar i två logaritmiska termer och en arcustangent ... Lite jobb återstår.

dr_lund skrev:
Jag skulle föreslå partialbråksansats, där jag ansätter
$\dfrac{1}{x(1+x^2)}=\dfrac{A}{x}+\dfrac{Bx+C}{1+x^2}$ ,
som landar i två logaritmiska termer och en arcustangent ... Lite jobb återstår.

Tack, men är inte riktigt med på varför 2:an i i nämnaren samt minustecknet försvinner när du gör partialbråksindelning. Sen är jag inte heller med på varför B är multiplicerat med x och varför C och B båda står i täljaren för termen $\frac{B x + C}{x^{2} + 1}$

Jag bryter ut dessa konstanter, de kommer såklart med i slutkalkylen.

Ang. Bx+C: Du har ett bråk vars nämnare inte går att faktorisera i reella förstagradare. Därav denna ansats.

Kolla gärna i din lärobok eller föreläsningsanteckningar om partialbråksuppdelning.

Jag gissar att detta är behandlat vid era genomgångar, eller hur?

dr_lund skrev:
Jag bryter ut dessa konstanter, de kommer såklart med i slutkalkylen.
Ang. Bx+C: Du har ett bråk vars nämnare inte går att faktorisera i reella förstagradare. Därav denna ansats.
Kolla gärna i din lärobok eller föreläsningsanteckningar om partialbråksuppdelning.
Jag gissar att detta är behandlat vid era genomgångar, eller hur?

Tack för förklaringen, jag är med på ovan nu. Det enda som jag dock undrar över är om det är nödvändigt att bryta ut dessa konstanter? Vad är syftet med att bryta ut konstanterna eg?

Jag testade men verkar ju inte få samma svar.

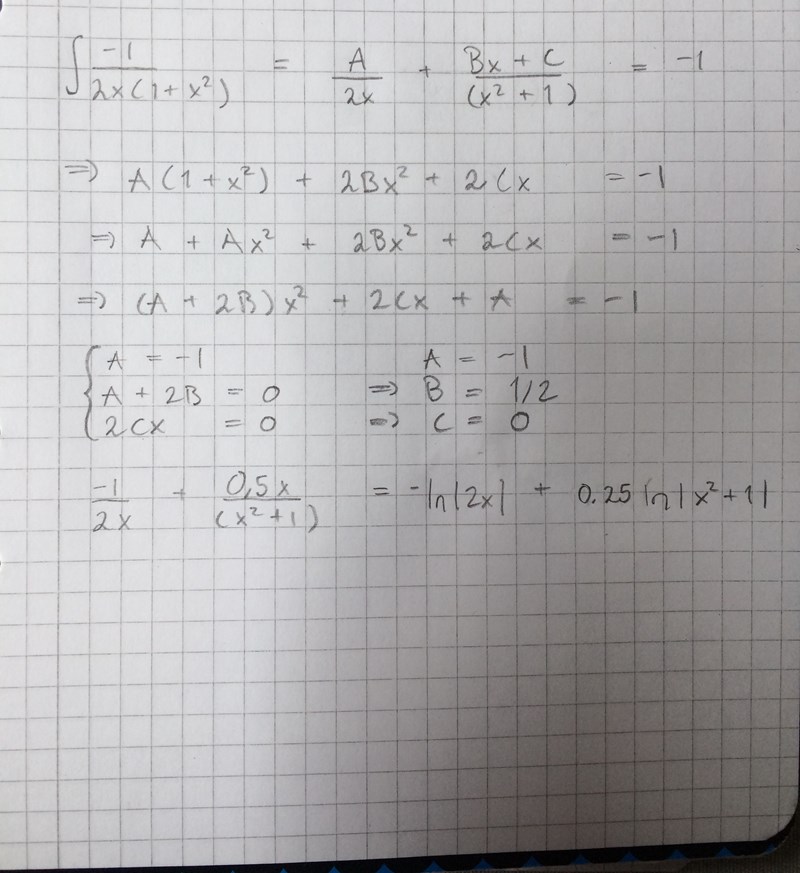
Nej det är såklart en option. Jag tycker det bir enklast så

dr_lund skrev:
Nej det är såklart en option. Jag tycker det bir enklast så

Okej.

Svara

Visa senaste svar