Partialintegration med samtliga primitiver
Bestäm med hjälp av partialintegration samtliga primitiver till
a) e^(x) * sin(x)
b) e^(2x) * sin(3x)
Har problem med denna uppgift, enligt tipset i boken ska man integrera två gånger men förstår inte varför. Finns det något sätt att ¨se¨ att funktionen måste integreras två gånger?
T.ex. skulle x^(2)*cos(x) behöva integreras två gånger men x*cos(x) behöva integreras en gång. finns det något liknande i denna fråga?
Eftersom sin(x) och cos(x) är varandras derivata så kommer man tillbaka till ursprungsfunktionen (med undantag för tecken mm) genom att derivera/integrera 2 gånger. Det är väldigt användbart i dessa uppgifter.
Tack för förklaringen, men om man skulle ta x*cos(x) skulle detta inte funka. Är det för att man får en positiv integral?
Du ska ju använda partialintegration, dvs från produkten av två funktioner uv är derivatan d(uv)=udv+vdu, därav och här med : 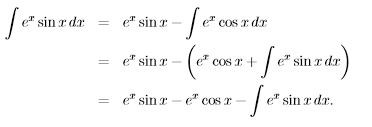 - alltså två (partiella) integrationer. Därifrån kan du få ut svaret.
- alltså två (partiella) integrationer. Därifrån kan du få ut svaret.
HT-Borås skrev :Du ska ju använda partialintegration, dvs från produkten av två funktioner uv är derivatan d(uv)=udv+vdu, därav och här med :
- alltså två (partiella) integrationer. Därifrån kan du få ut svaret.
Förstår beräkningsmässigt hur det går till. I detta fall kan jag redan ta över från högerledets integral till vänsterledet eftersom att de är lika men det finns fall då det krävs fler än två integreringar, betyder det att jag kan i allmänhet fortsätta integrera i en funktion tills att jag får ut det som står i vänsterledet?
Nej, det är ett väldigt ovanligt trick som bara fungerar med exponentialfunktion gånger trigonometrisk funktion.


