Partiella derivator
Hej, jag löste typ del a av uppgiften med kedjeregeln men verkar inte kunna hitta en primitiv funktion till funktionen i del b
här är uppgiften:
så här löste jag a):

så här långt kom jag på b):
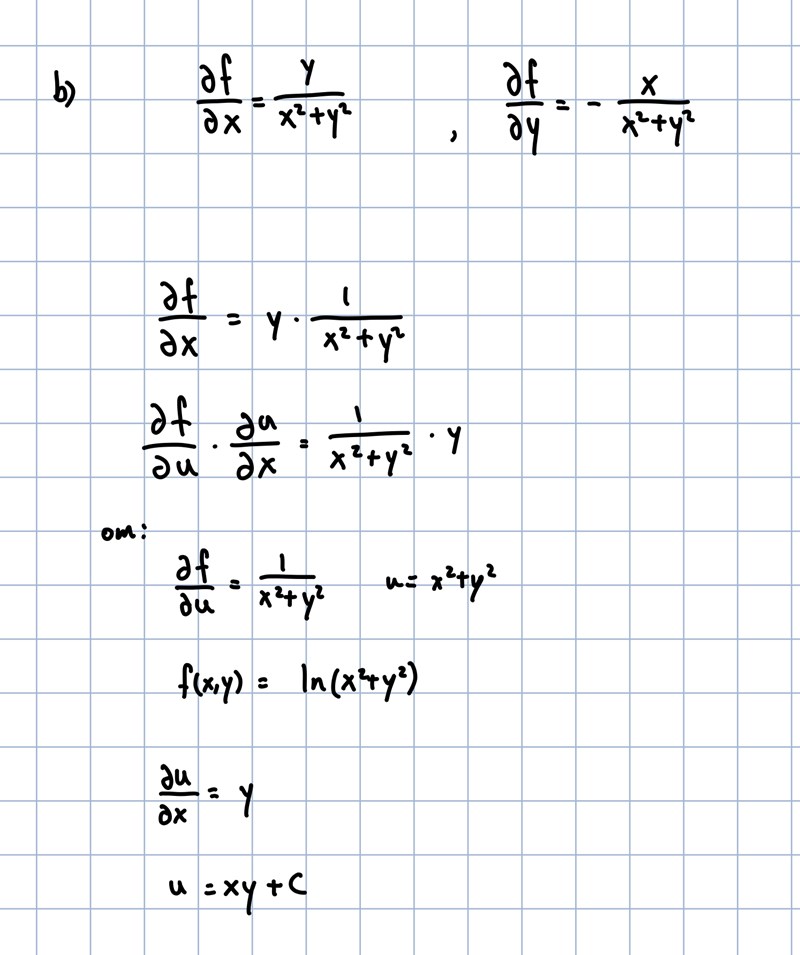
hur kan jag hitta den primitiva funktionen?
Prova att förkorta bråket med y^2 och se om du känner igen resultatet från någon deriveringsregel. Tänk arcus!
Skaft skrev:Prova att förkorta bråket med y^2 och se om du känner igen resultatet från någon deriveringsregel. Tänk arcus!
Jaa, arctan! Tack!
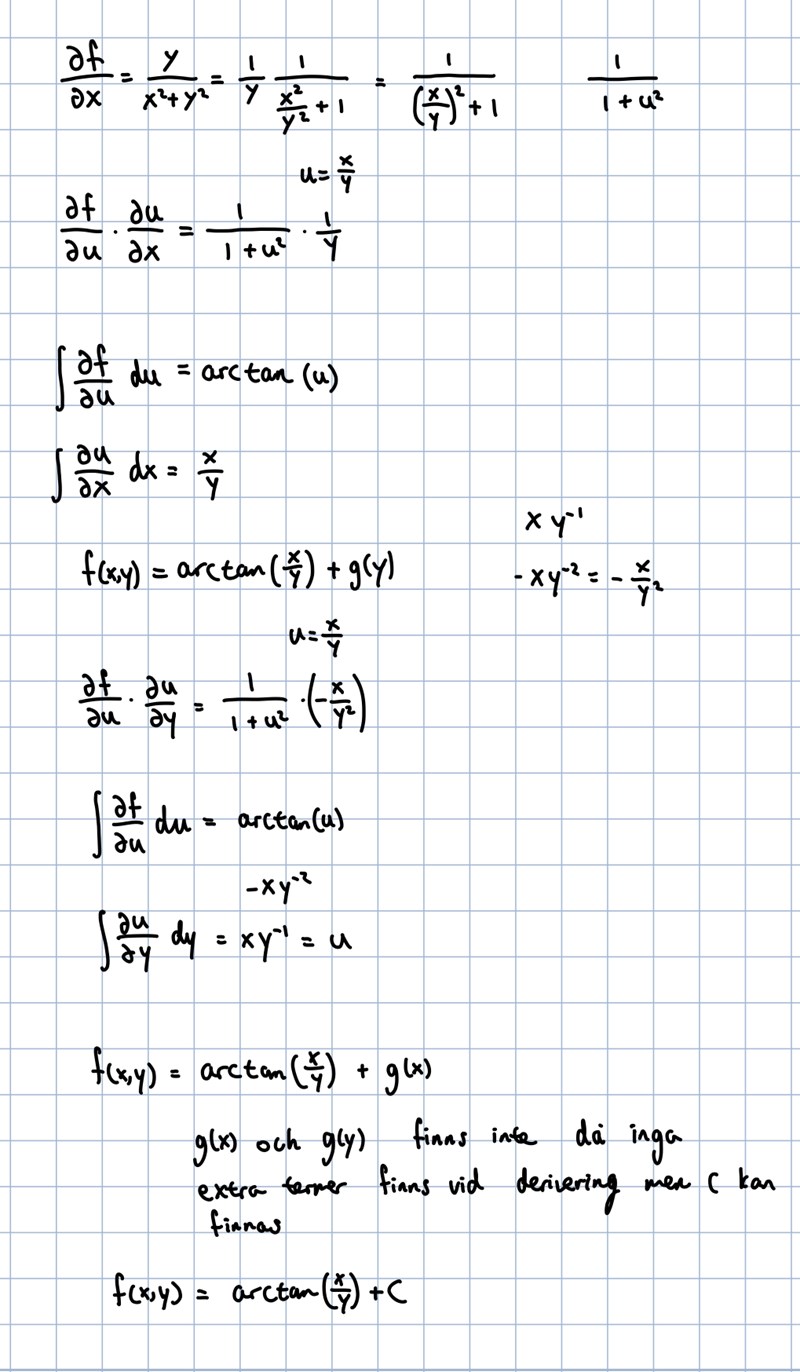
Är det så man ska lösa uppgiften eller finns det bättre metoder för att ”se” funktionen?
Efter att du kommit fram till att
så måste du komma ihåg att inte försvinner i deriveringen, eftersom du deriverar med avseende på y. Jag är faktiskt inte riktigt säker på vad som händer där, du verkar integrera tillbaka (trots att du redan hittat arctan). Istället kan du använda uttrycket för som du hittat, derivera det (och derivatan innehåller då ) och likställa den derivatan med den som är given i uppgiften. På så sätt kan du lösa ut att , och därigenom dra slutsatsen att .
Skaft skrev:Efter att du kommit fram till att
så måste du komma ihåg att inte försvinner i deriveringen, eftersom du deriverar med avseende på y. Jag är faktiskt inte riktigt säker på vad som händer där, du verkar integrera tillbaka (trots att du redan hittat arctan). Istället kan du använda uttrycket för som du hittat, derivera det (och derivatan innehåller då ) och likställa den derivatan med den som är given i uppgiften. På så sätt kan du lösa ut att , och därigenom dra slutsatsen att .
Ah, jag vet inte hur man löser uppgiften på ett bra sätt så jag tänkte att man kunde integrera det andra uttrycket också för att få f(x,y) och försöker visa att man kommer fram till arctan(x/y) från båda villkoren. Men om jag har förstått dig rätt så kan man istället derivera uttrycket vi får från som är arctan(x/y) + g(y) och derivera med avseende på y och får + g´(y) och sedan jämföra med villkoret vi får och säger att g(y) kan endast vara em konstant C?
Ja, eller istället för att "jämföra" med villkoret som givits föreslår jag att du likställer derivatan med det. Det är ju två uttryck för samma sak, de ska vara lika. På så sätt kan du bestämma g'(y) genom att lösa ekvationen som uppstår, istället för att behöva resonera i ord.
Använd polära koordinater så blir det inte så mycket räknande.
Skaft skrev:Ja, eller istället för att "jämföra" med villkoret som givits föreslår jag att du likställer derivatan med det. Det är ju två uttryck för samma sak, de ska vara lika. På så sätt kan du bestämma g'(y) genom att lösa ekvationen som uppstår, istället för att behöva resonera i ord.
Ja det är sant, man kan ju sätta likhet och lösa ut g´(y) = 0. Tack för hjälpen!
Jroth skrev:Använd polära koordinater så blir det inte så mycket räknande.
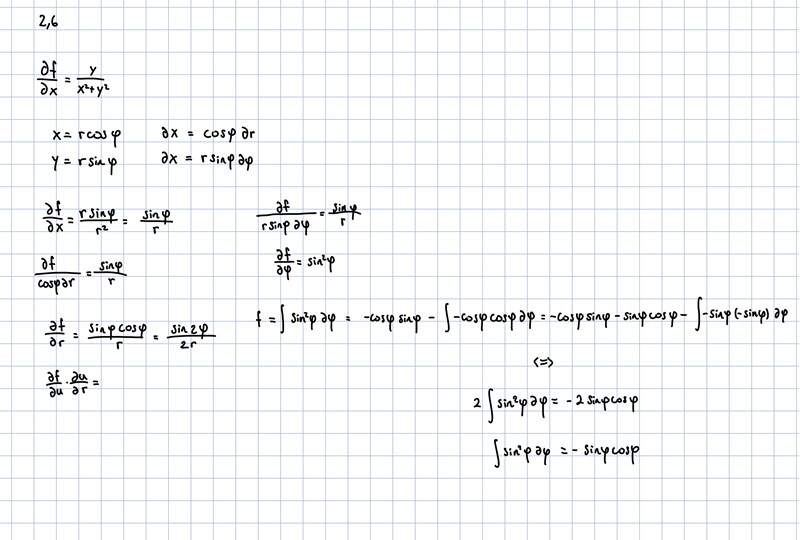
hmm, blev lite konstigt när jag försökte göra det, det är väl så man utför variabelbyte för partiella derivator?
Eftersom gäller att:
Qetsiyah skrev:Eftersom gäller att:
Hello! :D
Förstår inte riktigt varför arctan(x) + arctan(1/x) = konstant ger f(x,y) = arctan(x/y) + K
Säger du att g(y) är -arctan(y/x) och får ut en konst till första ekvationen när du byter ut g(y)?
Enligt uppgiften är
Jämför vi med gradienten i polära koordinater ser vi att
Dessa uttryck för ska gälla samtidigt. Det enda lösningen är (med en godtycklig konstant C)
Jroth skrev:Enligt uppgiften är
Jämför vi med gradienten i polära koordinater ser vi att
Dessa uttryck för ska gälla samtidigt. Det enda lösningen är (med en godtycklig konstant C)
Tack, hur får vi fram gradienten i polära koordinater? På , är ditt ?
Zeshen skrev:Tack, hur får vi fram gradienten i polära koordinater? På , är ditt ?
Jag svarar på din andra fråga först. Det du säger stämmer. Enhetsbasvektorerna i polära koordinater är
Gradienten av det skalära fältet f i polära koordinater ges av
Det är så viktigt att kunna utantill att jag gör en rektangel runt! Vill man själv bevisa saken använder man t.ex. kedjeregeln för derivation av en sammansatt funktion samt uttrycken för enhetsbasvektorerna ovan:
Andra sätt att hålla ordning på gradienten är att känna till skalfaktorerna för transformationen, eller genom att använda den kontravarianta basen. Men det lättaste är att slå upp den i Beta!
Jroth skrev:Zeshen skrev:Tack, hur får vi fram gradienten i polära koordinater? På , är ditt ?
Jag svarar på din andra fråga först. Det du säger stämmer. Enhetsbasvektorerna i polära koordinater är
Gradienten av det skalära fältet f i polära koordinater ges av
Det är så viktigt att kunna utantill att jag gör en rektangel runt! Vill man själv bevisa saken använder man t.ex. kedjeregeln för derivation av en sammansatt funktion samt uttrycken för enhetsbasvektorerna ovan:
Andra sätt att hålla ordning på gradienten är att känna till skalfaktorerna för transformationen, eller genom att använda den kontravarianta basen. Men det lättaste är att slå upp den i Beta!
Ah, coolt sätt att lösa uppgiften på! 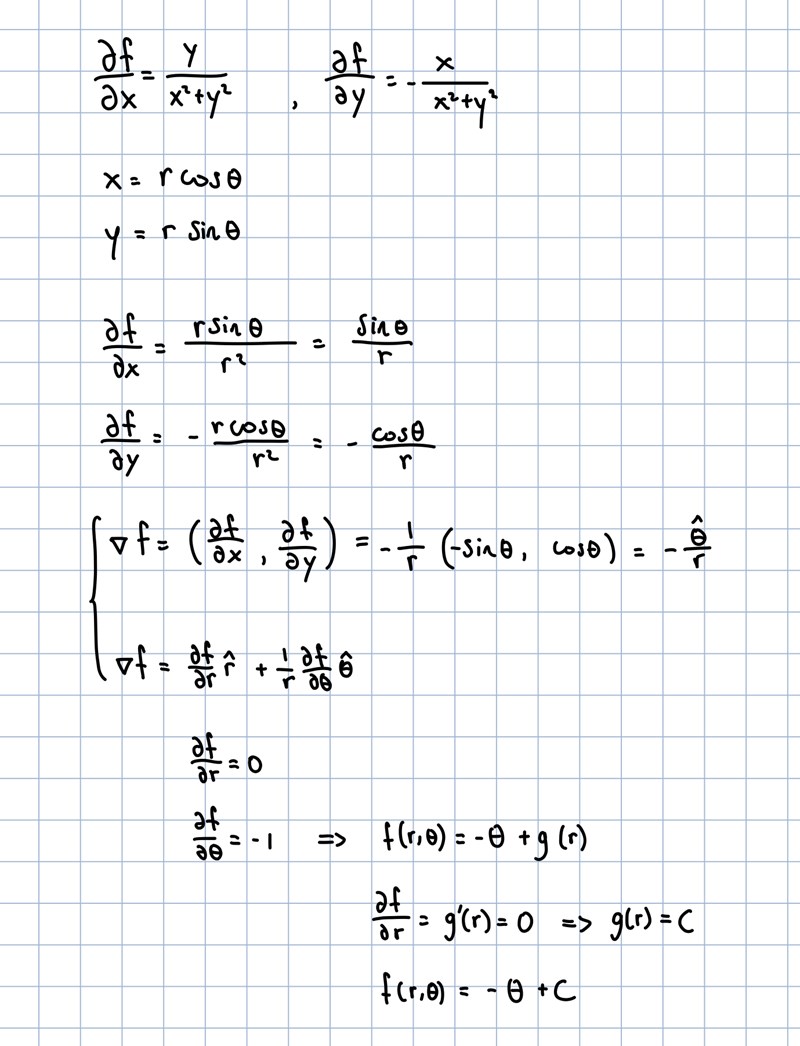
Fast sättet att skriva gradienten som enhetsvektorer och sen byta bas som transformation tror jag inte vi har gått igenom riktigt. Skulle du kunna visa hur du får fram ? Om du vill får du visa hur man bevisar det som står i rektangel med kedjeregeln för derivation av sammansatta funktioner och uttrycken av enhetsbasvektorerna. Den kontravarianta basen har jag inte hört talats om, vilken kurs är läser man om den?
Zeshen skrev:Skulle du kunna visa hur du får fram ?
Tanken med polära koordinater är att man istället för att ange ett x- och ett y-värde för en punkt någonstans i planet anger dess avstånd, , till ett origo och den vinkel som bildas med (någon) tänkt referensaxel.
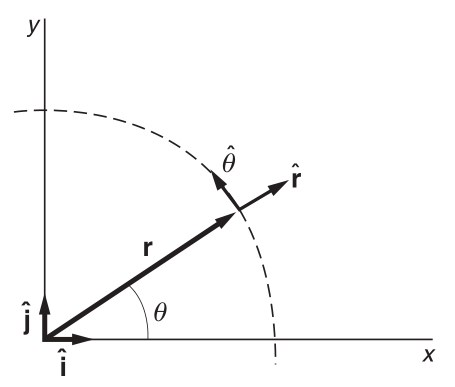
Vi lägger in två vinkelräta basvektorer av enhetslängd, och i punkten (se bild). Det är viktigt att inse att basvektorerna pekar i olika riktningar i olika punkter, men de är alltid vinkelräta mot varandra. Enkel komposantuppdelning ger oss komponenterna i x- och y-led.
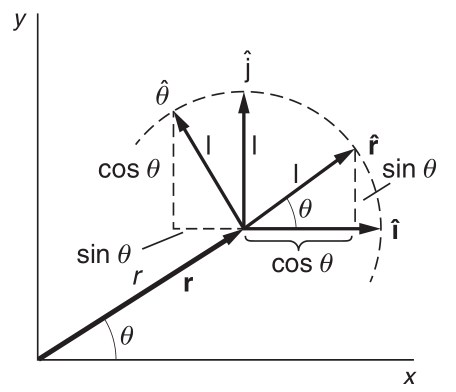
och
För att övertyga sig om att det här verkligen fungerar kan man testa att beräkna längden av vektorerna samt kontrollera att de är vinkelräta mot varandra oavsett i vilken punkt man är, dvs
Om plan- och rymdpolära koordinater lär man sig oftast under de inledande matematik- och fysikkurserna (t.ex. flervariabel).
Jroth skrev:Zeshen skrev:Skulle du kunna visa hur du får fram ?
Tanken med polära koordinater är att man istället för att ange ett x- och ett y-värde för en punkt någonstans i planet anger dess avstånd, , till ett origo och den vinkel som bildas med (någon) tänkt referensaxel.
Vi lägger in två vinkelräta basvektorer av enhetslängd, och i punkten (se bild). Det är viktigt att inse att basvektorerna pekar i olika riktningar i olika punkter, men de är alltid vinkelräta mot varandra. Enkel komposantuppdelning ger oss komponenterna i x- och y-led.
och
För att övertyga sig om att det här verkligen fungerar kan man testa att beräkna längden av vektorerna samt kontrollera att de är vinkelräta mot varandra oavsett i vilken punkt man är, dvs
Om plan- och rymdpolära koordinater lär man sig oftast under de inledande matematik- och fysikkurserna (t.ex. flervariabel).
Tack så mycket! Kanske förstår mer nu efter att ha läst lite mer. Jag har fortfarande svårt för linjär algebra för koncepten är mindre intuitiva och ”bildliga”. Kommer vara jobbigt sen när jag kommer till kvantmekaniken.
Känner igen det från mekaniken med cylinderkoordinater(i detta fall 0 i z komponenten) och kraftekvation vid rörelser med krökning!
Det du har gjort är alltså att se f som en skalär funktion av flervar och sedan skalär multiplicerat med nablaoperatorn (vilket är en vektor?) vilket blir grad f dvs. ett fält av grandienter i koordinatsys.. Ifall vi utför det på en vektoriell funktion så fås divergensen & rotationen för skalär och vektorprodukt.
Vad är nablaoperatorn för något egentligen (en vektor eller en operation?) och hur kom man ens på det? Verkar ha mycket med fält och flöde att göra. (Flervarre boken nämner bara kort hur man kan använda det)
Zeshen skrev:
Tack så mycket! Kanske förstår mer nu efter att ha läst lite mer. Jag har fortfarande svårt för linjär algebra för koncepten är mindre intuitiva och ”bildliga”. Kommer vara jobbigt sen när jag kommer till kvantmekaniken.
Ja och typ allt möjligt annat, linalg är viktigt.
Det du har gjort är alltså att se f som en skalär funktion av flervar och sedan skalär multiplicerat med nablaoperatorn (vilket är en vektor?) vilket blir grad f dvs. ett fält av grandienter i koordinatsys.. Ifall vi utför det på en vektoriell funktion så fås divergensen & rotationen för skalär och vektorprodukt.
Yes? I detta fall är f skalärvärt så multiplikation med nabla ger återigen en vektor.
Vad är nablaoperatorn för något egentligen (en vektor eller en operation?) och hur kom man ens på det? Verkar ha mycket med fält och flöde att göra. (Flervarre boken nämner bara kort hur man kan använda det)
Ja såklart det har med fält och flöde att göra. Man kallar det för en operator för att den egentligen producerar en ny funktion av en befintlig (vektorvärd eller skalärvärd) genom multiplikation, skalärprodukt eller kryssprodukt. Det finns lite vektornalays i flervariabelkursen. Kolla även laplaceoperatorn https://sv.m.wikipedia.org/wiki/Laplaceoperatorn




