Partikulär lösning
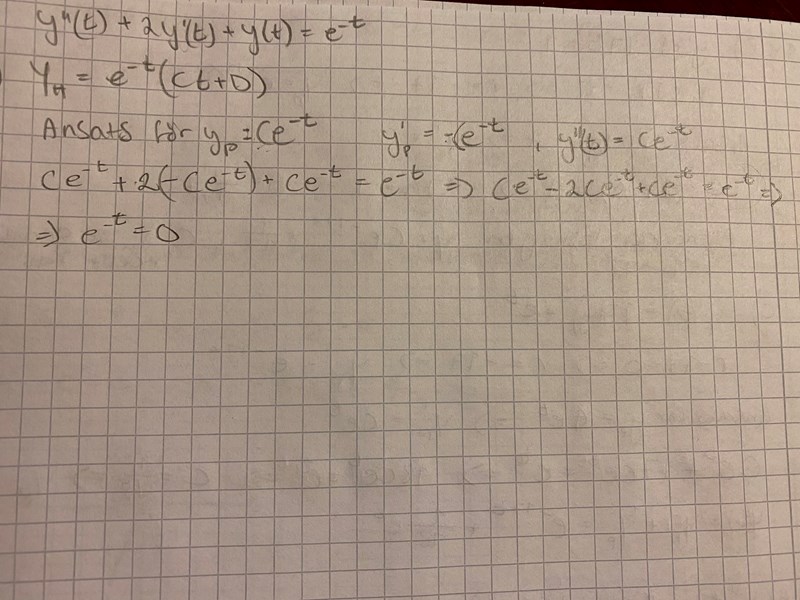
jag ska lösa differentialekvationen som står högst upp på bilden. Förstår inte hur jag ska få till partikulär lösningen. Något blir fel, då facit har skrivit detta som svar
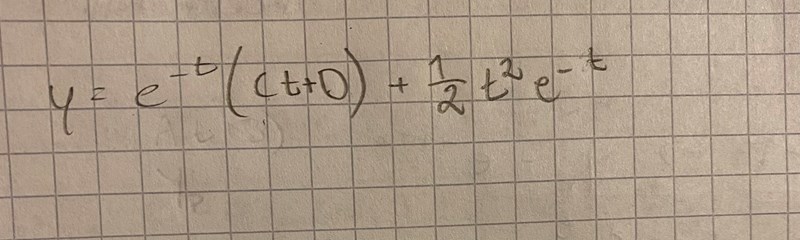
står det verkligen ct+0 i parantesen?
Prova istället, det blir nog lite enklare. Annars blir det rätt enkelt med Laplace men antar att ni inte gått igenom det?
Förlåt, det är jag som skriver otydligt. Den där "nollan" är ett D. Så det står (Ct+D). Men det blir ju samma sak med den partikulärlösningen. Får det även där 0 på VL 😪
Kommer du vidare då? Nu har vi alltså löst den karakteristiska ekvationen.
Efter detta kvarstår att göra en ansats, men teckan först ett uttryck för genom att lösa den karakteristiska ekvationen.
Ansätt yp(t) = z(t)e-t.
Vi får efter lite arbete att e-tz’’(t) = e-t, vilket ger att z’’(t) = 1, vilket ger z(t) = t2/2.
PATENTERAMERA skrev:Ansätt yp(t) = z(t)e-t.
Vi får efter lite arbete att e-tz’’(t) = e-t, vilket ger att z’’(t) = 1, vilket ger z(t) = t2/2.
Mycket riktigt, mitt första inlägg är lite tramsigt måste jag säga, vad ett bra tag sedan jag löste BVP etc utan att använda laplace så fick tänka till lite själv.
Nu har du iaf allt du behöver för att lösa diffen @ilovechocolate. :)
Dracaena skrev:
Kommer du vidare då? Nu har vi alltså löst den karakteristiska ekvationen.
Efter detta kvarstår att göra en ansats, men teckan först ett uttryck för genom att lösa den karakteristiska ekvationen.
Menar du såhär? 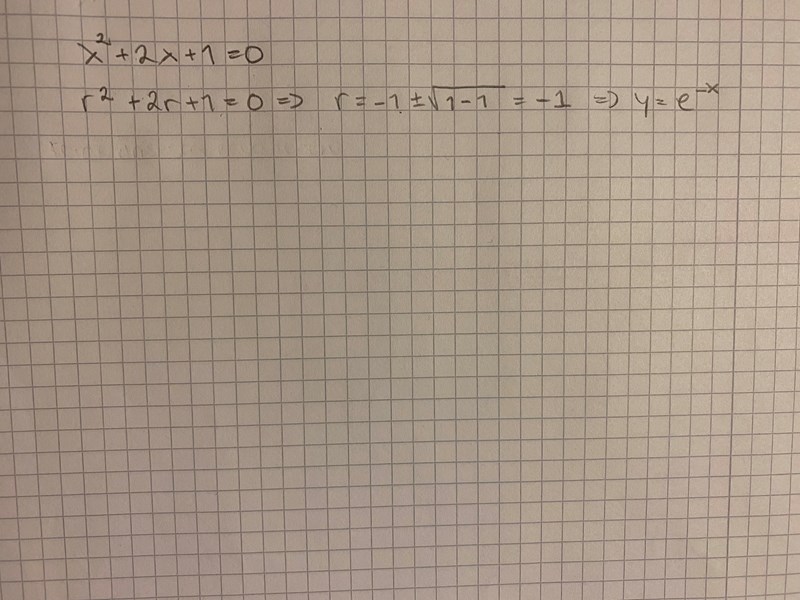 Eller är jag bara helt ute och cyklar nu? 🤔
Eller är jag bara helt ute och cyklar nu? 🤔
PATENTERAMERA skrev:Ansätt yp(t) = z(t)e-t.
Vi får efter lite arbete att e-tz’’(t) = e-t, vilket ger att z’’(t) = 1, vilket ger z(t) = t2/2.
Nu tappa du mig helt. Du ansätter yp som . Detta ger och . Hur kom du fram till resten? 😥
Du måste ta fram första samt andraderivatan och stoppa in i diffen.
Tillägg: 12 okt 2021 22:20
Notera att det inte är utan så att du måste använda produktregeln.
Precis som Dracaena säger.
(ze-t)’ = z’e-t - ze-t. Osv.
Typ såhär
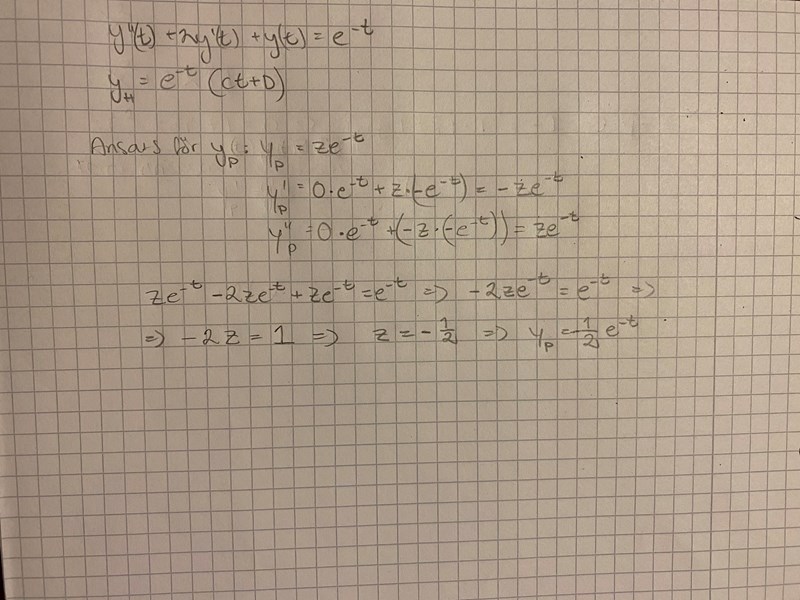 Fast det blev fortfarande inte riktigt rätt…
Fast det blev fortfarande inte riktigt rätt…
z är en funktion inte en konstant.
yp = ze-t
y’p = z’e-t - ze-t
y’’p = z’’e-t - z’e-t - z’e-t + ze-t
y’’p + 2y’p + yp = e-t =>
z’’e-t = e-t => z’’ = 1.
Okej! Men måste fråga då, varför har du lagt till ett z överhuvudtaget? Hänger inte riktigt med på det, och det är därför jag försöker få bort den 😅
Väldigt ofta blir det enklare att ansätta en funktion på formen z(t), om du inte vill så behöver du inte men eftersom du redan i din karakteristiska har så måste du multiplicera med t så att du isf måste ansätta vilket förmodligen kommer bli grisigare i detta fallet men det fungerar ju också om du vill det.
ilovechocolate skrev:Okej! Men måste fråga då, varför har du lagt till ett z överhuvudtaget? Hänger inte riktigt med på det, och det är därför jag försöker få bort den 😅
Titta här.


