Party girl och rotationsvolymer

Nu är jag fortfarande i roterande volymer :).

Jag har läst hur man räknar integraler som roterar kring x-axeln, och när det gäller rotation kring y-axeln, tror jag att jag har kommit på något som fungerar:

Till exempel, om vi försöker räkna ut integralen $\int_{1}^{4} x^{2}$ dx kring y axeln, man kan också tänka att det går att invertera x och y axeln, och isf blir $x^{2}$ en annan funktion.

http://sketchtoy.com/68236411

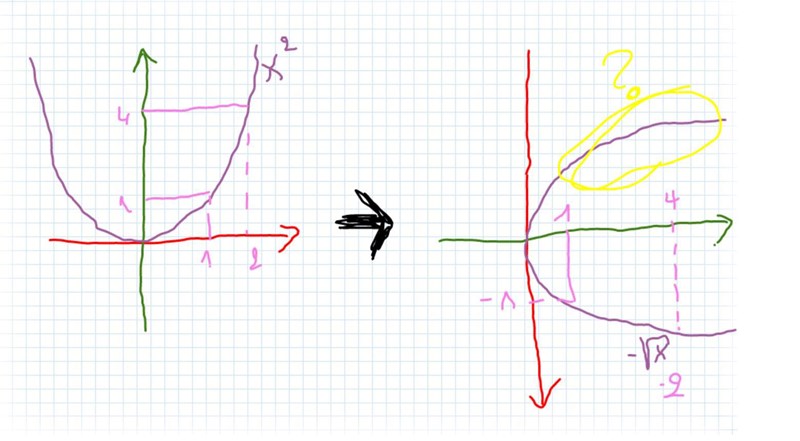
Och vad blir hon? 1 blir -1, 4 blir -2, 9 blir -3 osv, dvs $- \sqrt{x}$ !

Nu krävs det en stark suspend your disbelief moment, för jag ser väl att det är en del värde i gul som borde inte vara här (varje x ger 2 y...), så ''funktion'' är inte injektiv (som jag har lärt mig nyligen på pluggakuten :p) eller möjligt för den delen. Men iaf, vi säger att vi bryr oss inte om den gula delen.

Så vad blir volymen?

$π \int_{1}^{4} (- \sqrt{x})^{2} dx$ , dvs $π \int_{1}^{4} x d x$ dvs $π (\frac{4^{2}}{2} - \frac{1^{2}}{2}) = 7, 5 π$

Så det är lite grand som ett party girl som ramlar på marken mellan 2 fester, marken försvinner under föterna (jag menar x-axeln), allt som var vertikalt blir horizontalt (y axeln blir x axeln) och såklart livet som var jätte roligt en stund sedan suger nu för pengarna och mobilen (skärmen gick sönder, fan varför köp jag en Iphone!!) har rullat ur borsen och klänningen är förstörd (asså $x^{2} b l i r n u - \sqrt{x}$ ), en slags trist invers.

Jag har räknat med att derivera med avseende på y, $π \int_{1}^{4} y dy$ och det ger samma resultat eftersom integrerad y ger $\frac{y^{2}}{2}$ .

Så om man bortse från dom oppenbara problem av en x värde som ger två y värde, och säkert andra öppenbara problem som jag själv inte kan se, visst borde det kunna fungera? Det är väl bara att hitta varje funktion ''trist invers''? För potenser tror jag att jag vet (plus/minus byts framför x och a blir 1/a, eller tvärtom)

Enklare då att lära sig att integrera fram rotationsvolymer kring y-axeln.

Generellt avseende att integrera fram rotationsvolymer, oavsett om det gäller rotation kring x- eller kring y-axeln:

1. Rita figur, förstå vad de frågar efter.

2. Bestäm områdets gränser.

3. Välj integrationsmetod (skalmetoden/skivmetoden).

4. Finn ett uttryck för volymselementet dV.

5. Bestäm integrationsgränserna (från punkt 3).

6. Integrera.

7. Kontrollera/rimlighetsbedöm svaret.

8. Belöna dig själv för ett väl utfört arbete.

Jag gillar punkt 8.

Jo men det är lika bra att komma åt samma resultat på olika sätt :). Jag är ju en proffsigt slarvare, och bli lätt förvirrad av saker som liknar varandra. Jag hade jättesvårt med pq-formeln så jag behövde räkna samma sak under olika former :)

Och jag tycker att det är lite roligt med att leta trist invers av en funktion, det finns säkert en tabell nånståns?

Tack för checklisten !

Att beräkna volymen på ett annat sätt kan mycket väl vara ett sätt att utföra punkt 7.

På tal om punkt 7, det fungerar väl också med avstånd formeln för alla föremål som roterar kring y-axeln?

Jag var inte vacken i morse och började räckna en rotation kring y istället för en rotation kring x, och märkte att man kunde säkert integrera ${\sqrt{(x_{^{2}} - x_{1}) + (y_{2} - y_{1})}}^{2}$ . Y:or försvinner ju.

Daja skrev :
På tal om punkt 7, det fungerar väl också med avstånd formeln för alla föremål som roterar kring y-axeln?
Jag var inte vacken i morse och började räckna en rotation kring y istället för en rotation kring x, och märkte att man kunde säkert integrera ${\sqrt{(x_{^{2}} - x_{1}) + (y_{2} - y_{1})}}^{2}$ . Y:or försvinner ju.

Jag förstår inte hur avståndsformeln (som du för övrigt har skrivit av slarvfel) ska kunna användas här.

Yngve skrev :
Daja skrev :
På tal om punkt 7, det fungerar väl också med avstånd formeln för alla föremål som roterar kring y-axeln?
Jag var inte vacken i morse och började räckna en rotation kring y istället för en rotation kring x, och märkte att man kunde säkert integrera ${\sqrt{(x_{^{2}} - x_{1}) + (y_{2} - y_{1})}}^{2}$ . Y:or försvinner ju.
Jag förstår inte hur avståndsformeln (som du för övrigt har skrivit av slarvfel) ska kunna användas här.

Just det det saknas två kvadratter. Jag tänkte något i den här ändan:

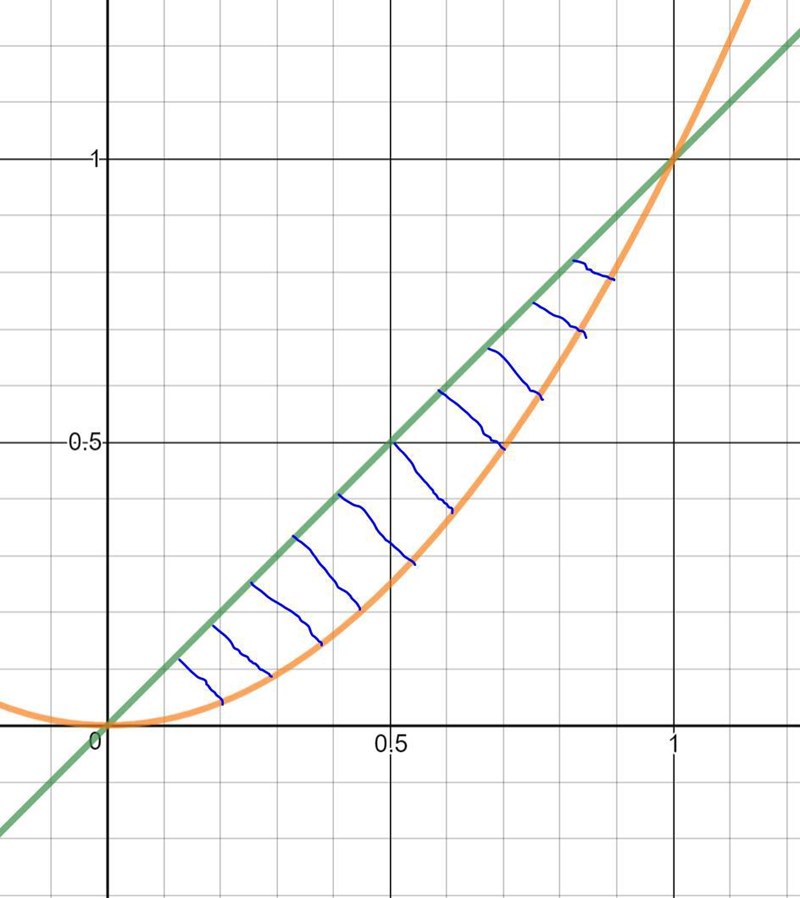
Beräkna den volym som uppstår när den randing ormåde roterar.

Vi letar efter en ormåde mellan 2 kurvor, dvs:

$π \int_{0}^{1} (x)^{2} d x - π \int_{0}^{1} (x^{2})^{^{2}} dx$

Som blir $π \int_{0}^{1} x^{2} - x^{4}$ dx

Med om vi använder avstånd formel, mellan varje punkt på y=x och $y = x^{2}$ , får vi $\sqrt{(x_{2} - x_{1}) + (y_{2} - y_{1})}$ . Vi kan strunta på alla y som har samma värde.

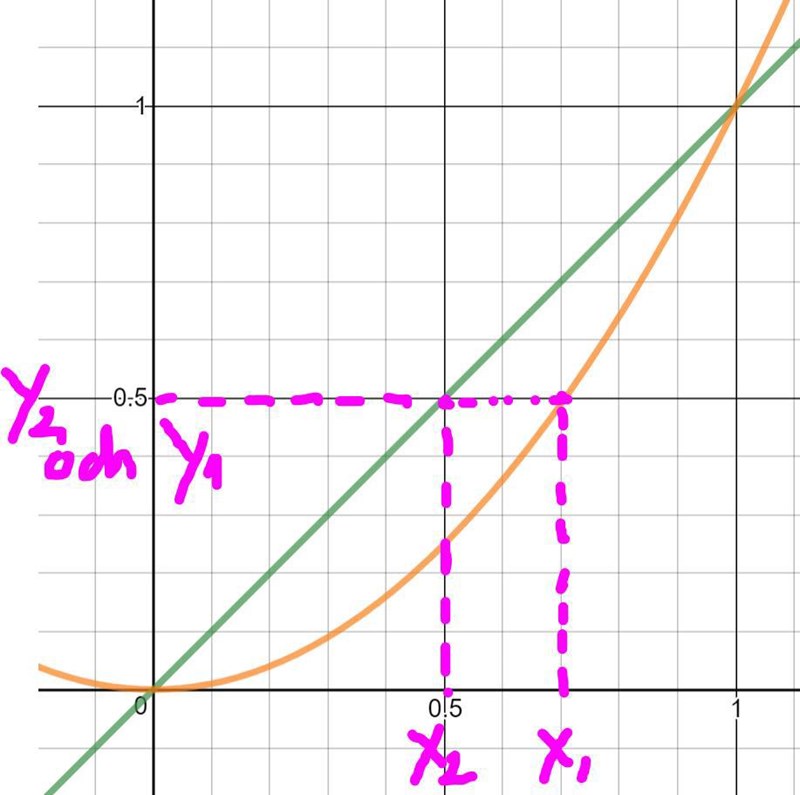
Så om vi sätter avståndformeln i vår integral blir det $π \int_{0}^{1} {\sqrt{(x_{2} - x_{1})}}^{2} d x$ som blir $π \int_{0}^{1} (x_{2})^{2} - (x_{1})^{2} d x$ , i den här fallet om vi ersätter $x_{2} m e d y = x$ och $x_{1} m e d y = x^{2}$ , blir det $π \int_{0}^{1}$ $x^{2} - x^{4}$ dx.

Men eftersom det saknades en kvadrat fukar det inte, dessutom tog jag ut radien $x^{2}$ , och jag tror att det motsvarar rotation kring y axeln, så en borde integrera med respect to y. Så det funkar nog inte.

Svara

Visa senaste svar