Pendelns maximala hastighet

Du lyckades beräkna pendelns längd, menar du?

I kapitlet där denna uppgift är hämtad har lösningen för harmonisk svängning hos en pendel presenterats. Denna har formen:

$y = A\sin(\omega t+\varphi)$

Där $y$ är elongationen, $A$ är amplituden, $\omega$ är vinkelhastigheten, $t$ är tiden och $\varphi$ är fasvinkeln.

Detta typ av uttryck kan du använda dig av.

Ebola skrev:

Du lyckades beräkna pendelns längd, menar du?

I kapitlet där denna uppgift är hämtad har lösningen för harmonisk svängning hos en pendel presenterats. Denna har formen:

$y = A\sin(\omega t+\varphi)$

Där $y$ är elongationen, $A$ är amplituden, $\omega$ är vinkelhastigheten, $t$ är tiden och $\varphi$ är fasvinkeln.

Detta typ av uttryck kan du använda dig av.

Ja, jag har lyckats beräkna pendelns längd. Men hur ska man beräkna amplituden i så fall?

Och den formeln jag har fått av läraren är y=Asin($\omega$*t), så jag blir lite förvirrad med fasvinkeln. Jag vet inte vad det är och hur man ska få den. 

Jag ser nu att det är en pendel som svänger fram och tillbaka, inte upp och ned. Då är sambandet istället:

$\theta = \theta_0 \cos(\omega t)$

Där vi alltså släppt pendeln från en begynnelsevinkel $\theta_0$ vid tiden $t=0$. Vi beräknar trådens längd från att vi kan se perioden i grafen vilken också ges av: 

$T=2\pi \sqrt{L/g}$

Vad kan du säga om grafen? Om du tänker dig rörelsen hos pendeln enligt nedan (kraftigt överdriven vinkel):

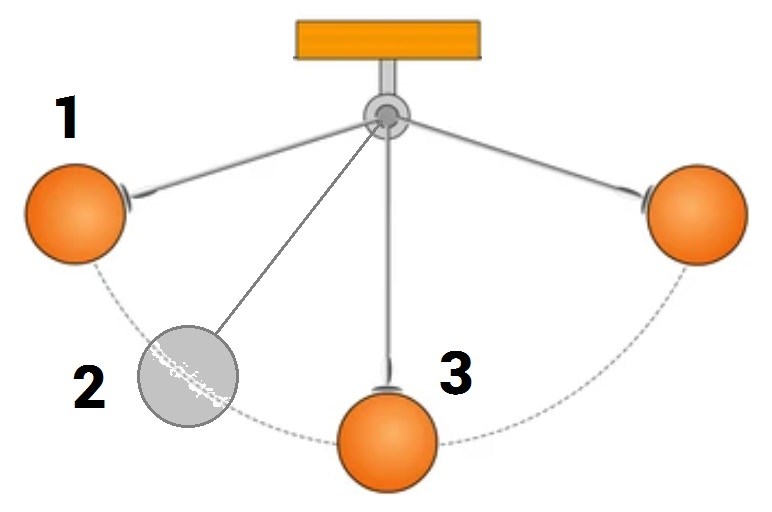
Kan du säga något om de olika punkterna? Vad är hastigheten i punkt 1, till exempel? I vilken av punkterna är den störst? Kan du säga något om kraften som snöret utsätts för vid de olika punkterna?

Sedan tittar du på grafen i uppgiften:

Vad kan du säga om punkterna A, B och C i grafen? Kan du matcha dessa punkter med punkterna under pendelns rörelse 1,2 och 3 i den andra bilden?

Ebola skrev:

Jag ser nu att det är en pendel som svänger fram och tillbaka, inte upp och ned. Då är sambandet istället:

$\theta = \theta_0 \cos(\omega t)$

Där vi alltså släppt pendeln från en begynnelsevinkel $\theta_0$ vid tiden $t=0$. Vi beräknar trådens längd från att vi kan se perioden i grafen vilken också ges av: 

$T=2\pi \sqrt{L/g}$

Vad kan du säga om grafen? Om du tänker dig rörelsen hos pendeln enligt nedan (kraftigt överdriven vinkel):

Kan du säga något om de olika punkterna? Vad är hastigheten i punkt 1, till exempel? I vilken av punkterna är den störst? Kan du säga något om kraften som snöret utsätts för vid de olika punkterna?

Sedan tittar du på grafen i uppgiften:

Vad kan du säga om punkterna A, B och C i grafen? Kan du matcha dessa punkter med punkterna under pendelns rörelse 1,2 och 3 i den andra bilden?

är kraften i tråden maximalt när kulan är i punkt 3, eller har jag tänkt helt fel?

Nej, du har inte tänkt fel, det är helt rätt. Om du någon gång åkt Loke på Liseberg så har du känt av hur mycket större normalkraft från stolen du utsätts för i den punkten hos attraktionens pendelrörelse.

Detta betyder alltså att Punkt 3 i pendelns rörelse matchas med punkt A i grafen. Var tror du att kraften i snöret är lägst? Denna animation kan hjälpa:

Där alltså $T$ är spännkraften i snöret. Genom att lista ut vilken punkt i din graf som korresponderar till punkt 1 i pendelns rörelse kan vi beräkna amplituden därför att detta är punkten där hastigheten är noll:

Om du alltså tittar på krafterna som pendeln utsätts för i läge 1 får du:

Där vi har att hastigheten $v$ är noll vilket ger:

$F-mg\cos\left(\theta_0\right) = \dfrac{mv^2}{L} = 0$

Så om jag förstår det hela rätt så är hastigheten = 0 i punkten 1 (vilket motsvarar punkten C i grafen) och hastigheten är maximalt i punkten 3? Och därifrån kan man räkna ut både amplituden och hastigheten. 

Ebola skrev:

Jag ser nu att det är en pendel som svänger fram och tillbaka, inte upp och ned. Då är sambandet istället:

$\theta = \theta_0 \cos(\omega t)$

Men jag undrar var kommer denna formel ifrån?

bellisss skrev:

Så om jag förstår det hela rätt så är hastigheten = 0 i punkten 1 (vilket motsvarar punkten C i grafen) och hastigheten är maximalt i punkten 3? Och därifrån kan man räkna ut både amplituden och hastigheten. 

Ja, exakt. Du får amplituden eller största vinkeln på rörelsen uppmätt från vertikalen (läge 3) till där hastigheten är noll (läge 1) från kraftjämvikten. Alltså:

$\theta_0 = \cos^{-1}\left(\dfrac{F}{mg}\right)$

Där kraften $F$ är den som du ser i punkt C i grafen. Sedan får du maximal hastighet från centripetalkraften som är störst vid läge 3 för pendeln eller A i grafen:

$F-mg\cos\left(\theta\right) = \dfrac{mv^2}{L}$

Men jag undrar var kommer denna formel ifrån?

Den beskriver vinkeln relativt vertikalen som funktion av tiden. Man brukar härleda den för en pendel av denna typ. Den andra relationen du skrev upp är för en massa som hänger i en fjäder och svänger vertikalt. De är dock synonymer då de båda beskriver harmonisk svängning.