Pendlar


hejsan
Jag skulle behöva ha hjälp med uppgiften.
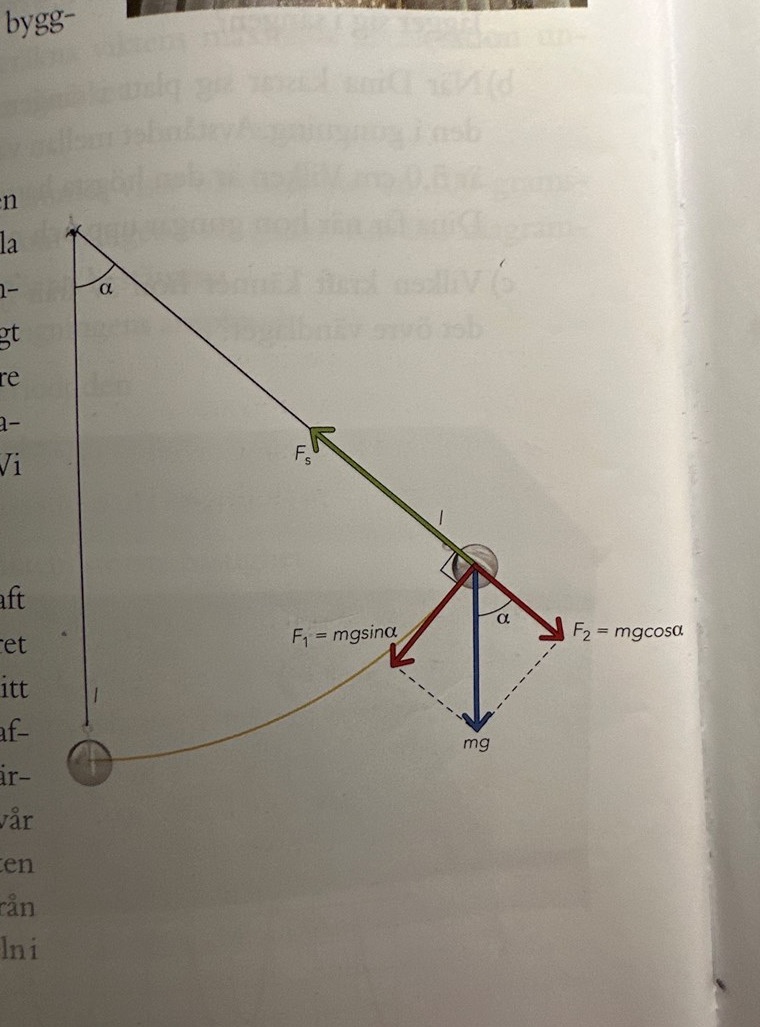
oklart om min figur är korrekt i relation till radien 200 m
F1 är centripetalkraften riktad mot kurvbanans centrum?
Fc=(mv2)/r
Du kan prova med tangens av vinkeln som är en kvot, alltså den mellan krafterna som verkar på pendeln: tyngdkraften och centripetalkraften. Lös sedan ut hastigheten.
Kan inte riktigt se varför just tangens och inte sinus.
tyngdkraften har komposantuppdelats
tyngdpunkten är väl känd?
och vinkeln mellan centripetalkraften och tygbdpunkten är väl 65 grader
Jag ser det så här, med en fiktiv centrifugalkraft Fc=(mv2)/r. (Inte så skalenligt ritat förstås.)
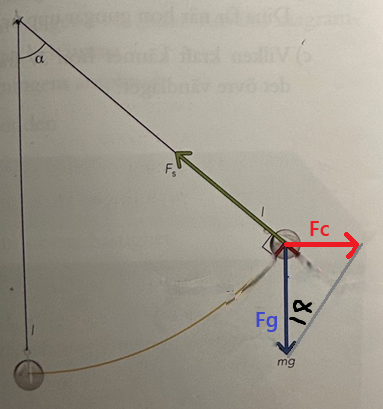
Då kan man se sambandet med tangens som Magnus O föreslår.
Så man behövde aldrig komposant uppdela tyngdkraften Fmg.
Utan man ska kunna se att kraften i snöret Fs och tyngdkraften Fmg har en resultatkraft FR. Och i detta fall är resultatkraft FR riktad inåt mot centrum, därav är resultantkraften lika med centripetalkraften, Fc=FR.
Japp! Så tänker jag. Personligen tycker jag det är tydligare att rita en centrifugalkraft, som drar pendeln utåt/uppåt, även om jag förstås vet att den inte finns. Förresten får jag ca 30 m/s, vilket verkar vara en hastighet ett tåg kan hålla i en kurva.


