Phytagorassats
Hej!
Behöver hjälp med 4262) Har även infogat hur jag tänkt än så länge men har kört fast...
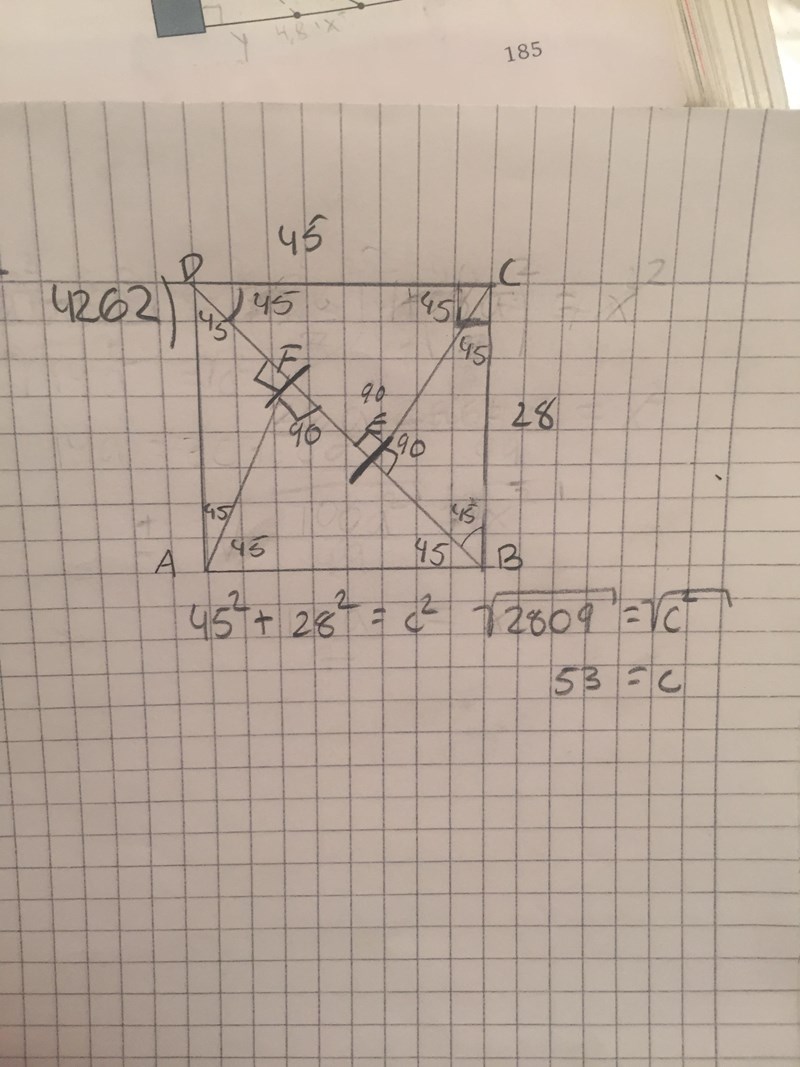
Det stämmer inte att vinklarna är som du har ritat ut.
Ett tips är att använda likformighet för att bestämma sidorna och .
Hej
Använd dig av tomast80 tips men tänk sen på att triangeln ABF och ABD är likformiga.
tomast80 skrev :Det stämmer inte att vinklarna är som du har ritat ut.
Ett tips är att använda likformighet för att bestämma sidorna och .
Okej, stämmer hypotenusan då? Kan jag på något sätt använda mig utav den?
Ja den stämmer, Om du säger att sträckan . Vad blir då uttrycket för sträckan FE?
jonis10 skrev :Ja den stämmer, Om du säger att sträckan . Vad blir då uttrycket för sträckan FE?
Blir det då FE = DF - EB
Någon som kan hjälpa mig?? Har fortfarande inte klurat ut den...
Diagonalen ADB är . Diagonalen på FDA är 28. Därför är triangeln FDA en skalning av ADB med faktorn . Därför gäller det att
Sedan är |EB| lika stor som |FD| . Därför får man att längden FE är



