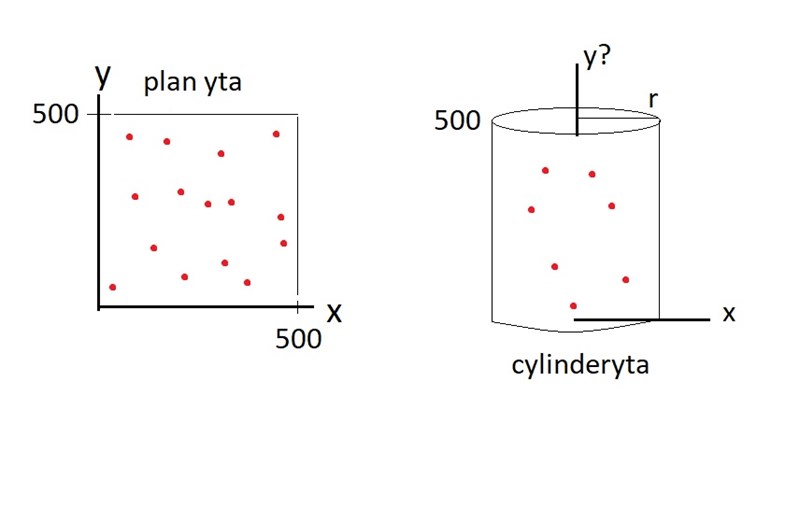
plan yta till cylinderyta

Hej,

Jag har ett sett av datapunkter i xy planet som är på en 500x500 plan kvadratisk yta. För att analysera datan behöver jag ha den på ytan av en cylinder istället för på en plan yta då datan ursprungligen är tagen från en cylinderyta. Jag vill beräkna avståndet mellan datapunkterna och om de är på en plan yta kommer punkterna längst ut verka ha långt avstånd fast dom egentligen är bredvid varandra. Tänk att ytan rullas ihop till en en cylinder runt y-axeln, där jag bara är intresserad av ytan på cylindern, inte botten och toppen av den. Min första tanke för att omvandla min data från en plan yta till cylinder var att göra om från kartesiska till cylindriska koordinater. Sen insåg jag att då jag beräknade radien och därefter omvandlade koordinaterna med följande ekv.:

$r = \sqrt{x^{2} +^{y^{2}}}$

$x = r \cos θ$

$y = r \cos θ$

så får jag ju olika värden på radien dvs. mina datapunkter hamnar inte på ytan av cylindern utan de hamnar på olika avstånd från axeln, vilket då inte bildar en cylinder eftersom cylindern har fast radie. Detta tänkte jag då lösa genom att jag använder dimensionerna för den första plana ytan, dvs. 500x500, och tänker att omkretsen på min tänkta cylinder är 500, vilket då ger en radie på

$r = \frac{o m k r e t s}{2 π}$ =79,6

och sen beräknar koordinaterna, så bör dom hamna på ytan av cylindern och inte på olika avstånd.

Mitt mål är att beräkna avståndet mellan datapunkterna på cylinderytan i höjd och längdled och därefter beräkna de med pythagoras sats, $a v s t å n d = \sqrt{l ä n g d^{2} + h ö j d^{2}}$ . För att få i höjdled tänkte jag därför använda proportionerna för plana ytan som har en höjd på 500, medan bredden tänkte jag räkna ut mha vinkeln mellan punkterna och därefter beräkna cirkelsegmentet

$L = r θ$

För att göra det behöver jag ha cylindern runt y-axeln, i och med att datan är given i kartesiska koordinater eller tänker jag fel? Det är ju en 2d yta från början, så vill jag j fortsätta ha en 2d yta i cylindern, alltså ingen z axel eller? All hjälp är uppskattad jag känner mig ganska förvirrad. Finns det något enklare sätt att göra det på?

Använd cylindriska koordinater. Alla punkter har samma radie, r = R.

Vill du ha avståndet fågelvägen eller längs cylinderytan?

Tack för svar. alla punkter har dock inte samma radie om jag beräknar r med ekvationen, här är ett exempel på några av koordinaterna för punkterna:

x=(368, 65, 380) (3 första x-koordinaterna på ytan)

y=(186, 189, 198)

r=(412.3348 ,199.8650, 428.4904)

som du ser så är radien olika för de olika värdena. jag tar alltså $r_{1} = \sqrt{{x_{1}}^{2} + {y_{1}}^{2}}$ osv för alla punkter, och det verkar som dom hamnar i planet för cylindern, alltså inte på ytan.

Jag vill ha avståndet på cylinderytan

Min tolkning var att du rullar ett "papper" som är 500 x 500 till en cylinder med höjd 500 och radie 500/(2π). Är det inte så?

jo det stämmer

Bra, då har alla punkter r = R = 500/(2π).

x får du omvandla till en vinkel, t.ex v = x/R.

Avstånd i v-led och y-led kan du då räkna ut mellan två punkter. Frågan är hur det resulterande totala avståndet blir.

EDIT: fast det kortaste avståndet längs cylinderytan är samma som för en rät linje på den utvecklade plana ytan.

tack! Så då om jag gör om alla x-koordinater och använder radien så borde det funka som en cylinder med höjden längs y-axeln?

okej men det är väl en approximation eller? med det kortaste avståndet på cylinderytan är rät linje på plan yta.

Det är exakt!

Ta två punkter på det utvecklade pappret. Kortaste vägen mellan punkterna är en rät linje.

Om du sedan knögglar ihop pappret är den tidigare räta linjen fortfarande närmsta vägen, om man måste röra sig längs pappret.

Om man gör en cylinder måste man dock undersöka om det blir närmare om man går "medurs" eller "moturs", eftersom man nu får periodiska randvillkor.

Du får alltså det kortaste av

$d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$

och

$d^2 = (500 - (x_2 - x_1))^2 + (y_2 - y_1)^2$

tack så mycket. jag undrar bara lite över v=x/R, ska det inte vara tan(v)=x/R? Eller tänker jag fel?

Gör som Dr.G föreslog, så slipper du bekymra dig.

Nej, inte tangens. x är egentligen längden av en bit cirkelsegment räknat från en startpunkt, så x = R*v.

Det saknas ett absolutbelopp i den sista ekvationen, men det märkte du nog.

(500 - |x2 - x1|)^2 + ...

Svara

Visa senaste svar