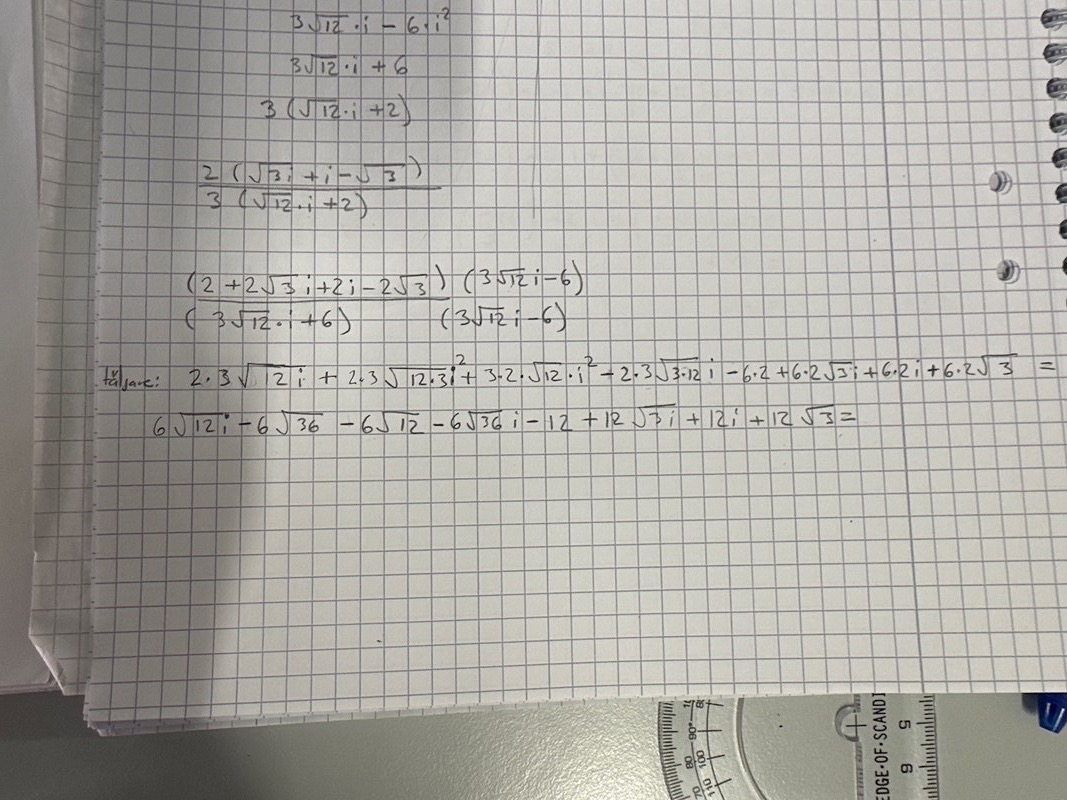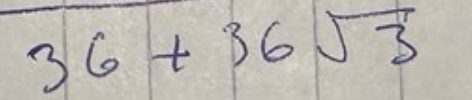Polär form

Ja, konjugatregeln för att fö bort i-komponenten i nämnaren är en strategi.

Jag själv skulle välja att istället skriva täljare och nämnare i polär for, och sedan förenkla med potensregler.

Hänger du med?

...eller jag skulle förmodligen också ha skrivit de två faktorerna i täljaren på polär form också, före förenkling med potensregler.

Jag har fastnat. Vet ej hur man ska gå vidare

Jag förklarade dåligt. Det jag menade var att det är förmodligen enklast att omvandla varje faktor i täljare och nämnare, till exponentiell form, sedan förenkla med potensregler, och till sist omvandla till polär form. 

Men vi kan testa din metod istället! 

Börja med nämnaren:

Konjugatet  till $3i(\sqrt{12}-2i)=6+3\sqrt{12}i$ är $6-3\sqrt{12}i$

Alltså ska du förlänga hela bråket med $6-3\sqrt{12}i$.

$(6-3\sqrt{12}i)(6-3\sqrt{12}i)=36+108=144$

Sedan täljaren:

Tänk på rubriksättningen @Biorr. Du kan exempelvis numrera dina trådar om polär form. /moderator 

Täljaren:

$(2+2i)(1+\sqrt{3}i)(6-3\sqrt{12}i)$

När jag tittar på den _tror_ jag att det kommer att bli snyggare ifall jag förenklar roten av tolv först)

$(2+2i)(1+\sqrt{3}i)(6-3\sqrt{12}i)=(2+2i)(1+\sqrt{3}i)(6-3\sqrt{3·4}i)=(2+2i)(1+\sqrt{3}i)(6-3·2\sqrt{3}i)=(2+2i)(1+\sqrt{3}i)(6-6\sqrt{3}i)=12(1+i)(1+\sqrt{3}i)(1-\sqrt{3}i)$

Kommer du vidare?

Kanske enklast att omvandla varje term till polär form

2+2i = 2$\sqrt{2}{e}^{i\pi /4}$  

1+$\sqrt{3}i$= $2e^{i\pi /3}$

osv och sedan är det bara att räkna ihop absolutbelopp och vinklar var för sig till, tror jag

$\frac{1}{3\sqrt{2}}{e}^{i\pi /4}$

hansa skrev:

Kanske enklast att omvandla varje term till polär form

2+2i = 2$\sqrt{2}{e}^{i\pi /4}$  

1+$\sqrt{3}i$= $2e^{i\pi /3}$

osv och sedan är det bara att räkna ihop absolutbelopp och vinklar var för sig till, tror jag

$\frac{1}{3\sqrt{2}}{e}^{i\pi /4}$

Håller med (fast jag får det till $\frac{\sqrt{2}}{3}e^{i\frac{\pi}{4}}$)

Yngve skrev:

hansa skrev:

Kanske enklast att omvandla varje term till polär form

2+2i = 2$\sqrt{2}{e}^{i\pi /4}$  

1+$\sqrt{3}i$= $2e^{i\pi /3}$

osv och sedan är det bara att räkna ihop absolutbelopp och vinklar var för sig till, tror jag

$\frac{1}{3\sqrt{2}}{e}^{i\pi /4}$

Håller med (fast jag får det till $\frac{\sqrt{2}}{3}e^{i\frac{\pi}{4}}$)

Jag tror att det där vanligtvis kallas exponentiell form, och att det som vanligtvis kallas polär form har formatet z=r(cosv+isinv). För att kunna använda den exponentiella formen av ett komplext tal behöver man först ha gått igenom Eulers formel (kom på mig själv i #7).

Jag har inte gått igenom Eulers formel ännu.

bara dettal

Biorr skrev:

Jag har inte gått igenom Eulers formel ännu.

bara dettal

Jag misstänkte det. Då är den strategi som du själv föreslog bäst. Dvs jobba med rektangulär form hela vägen, få bort i i nämnaren, och övergå till polär form i sista steget.

Behöver du mer hjälp från #10?

fick det här efter förenkling och konjugation , och nästa steg?

Kan du bryta ut 36 från nämnaren?

hur får jag vinkeln? Tan? Im =b och Re=a

Se Trinity2's lösning, och du får fram vinkeln med tangens, som det står i boksidan du kopierade in.

Men hur kunde du få detta i nämnaren i #16:

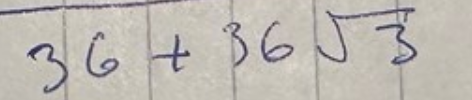
Om du direkt hade multiplicerat med den ursprungliga nämnarens komplexa konjugat skulle du ju ha fått ett reellt heltal. Vad hände? 

JohanF skrev:

Se Trinity2's lösning, och du får fram vinkeln med tangens, som det står i boksidan du kopierade in.

Men hur kunde du få detta i nämnaren i #16:

Om du direkt hade multiplicerat med den ursprungliga nämnarens komplexa konjugat skulle du ju ha fått ett reellt heltal. Vad hände? 

Vad har du gjort här?

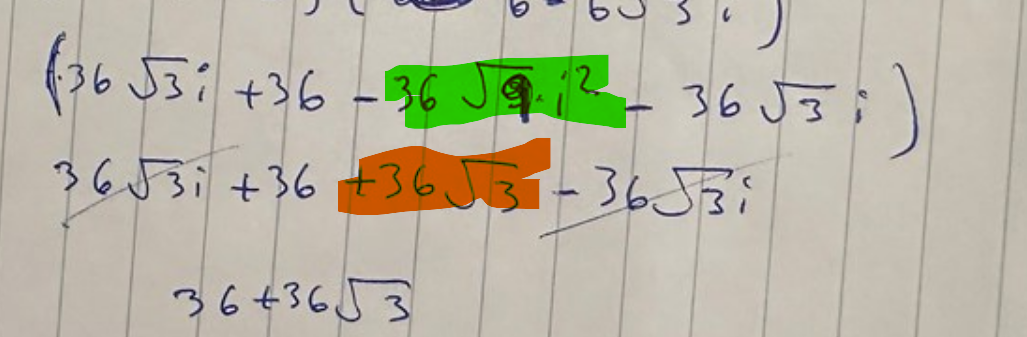
Skrev fel

Hur ska man jobba vidare då?

Jag tror du gjort något fel i tidigare steg, i täljaren också. Titta på stegen i #10 och se ifall du kan hitta det. 

JohanF skrev:

Täljaren:

$(2+2i)(1+\sqrt{3}i)(6-3\sqrt{12}i)$

När jag tittar på den _tror_ jag att det kommer att bli snyggare ifall jag förenklar roten av tolv först)

$(2+2i)(1+\sqrt{3}i)(6-3\sqrt{12}i)=(2+2i)(1+\sqrt{3}i)(6-3\sqrt{3·4}i)=(2+2i)(1+\sqrt{3}i)(6-3·2\sqrt{3}i)=(2+2i)(1+\sqrt{3}i)(6-6\sqrt{3}i)=12(1+i)(1+\sqrt{3}i)(1-\sqrt{3}i)$

 

Kommer du vidare?

Hur blir det 12(1+i)(1+√3i)(1–√3i) ?

Ser du att de två sista faktorerna i uttrycket också är komplexa konjugat till varandra?

Ja

$12(1+i)(1+\sqrt{3}i)(1-\sqrt{3}i)=12(1+i)·4$

Det här blev väldigt komplext… och rörigt. Gör så här istället

Trinity2 skrev:

Det här blev väldigt komplext… och rörigt. Gör så här istället

Vi har kommit fram till (2ggr) att använda exponentiell form är fusk i den här tråden.

Dividera täljare och nämnare med 2.

Du får (1+i)(1+√3i)/3i(√3-i) = (1/3)•(1+i)

Gör sedan om detta till polär form.

JohanF skrev:

Vi har kommit fram till (2ggr) att använda exponentiell form är fusk i den här tråden.

Men bryt då ut 2 från täljare och nämnare och så är du klar, om nu basal aritmetik är tillåtet… Att räkna med polär form är i 99 fall av 100 fullständigt idiotisk IMO.

Trinity2 skrev:

JohanF skrev:

Vi har kommit fram till (2ggr) att använda exponentiell form är fusk i den här tråden.

Men bryt då ut 2 från täljare och nämnare och så är du klar, om nu basal aritmetik är tillåtet… Att räkna med polär form är i 99 fall av 100 fullständigt idiotisk IMO.

Det var inte meningen att ordet "fusk" skulle uppfattas mer än bildligt. Ber om ursäkt för det. 

Det är inte svårare än att man i progressionen lär sig polär form före exponentiell form, och där är vi just nu. 

JohanF skrev:

Trinity2 skrev:

Visa föregående citat

JohanF skrev:

Vi har kommit fram till (2ggr) att använda exponentiell form är fusk i den här tråden.

Men bryt då ut 2 från täljare och nämnare och så är du klar, om nu basal aritmetik är tillåtet… Att räkna med polär form är i 99 fall av 100 fullständigt idiotisk IMO.

Det var inte meningen att ordet "fusk" skulle uppfattas mer än bildligt. Ber om ursäkt för det. 

Det är inte svårare än att man i progressionen lär sig polär form före exponentiell form, och där är vi just nu. 

Det är lugnt! (Text har inte det talade språkets nyanser och blir ofta "kantigt".)

Den polära formen är lömsk tycker jag. Den har inget logiskt aritmetiskt tankesätt. Det finns en annan tråd där TS upphöjer i 6 och får abs rätt men glömmer att multiplicera argumentet.

( r (cos t + i sin t) )^n =  r^n (cos nt + i sin nt)

är liksom inte aritmetiskt "naturligt" (och långt ifrån binomialutvecklingen...) men

( r e^(it) ) ^n = r^n e^(itn)

är det via de välkända potenslagarna, och dessutom trevlig att räkna med. 

Det är lugnt för mig också 😊! Jag håller helt med dig, komplexa tal i exponentialformsrepresentation is da shit! 

Nä, du gör något fel i täljaren innan du kommer till nedanstående bild:

För att vi ska kunna hjälpa dig att hitta ditt fel, så måste du visa de tidigare stegen som du har gjort i täljaren före ovanstående bild, annars blir det verkligen svårt att hitta.

$\frac{12(1+i)(1+\sqrt{3}i)(1-\sqrt{3}i)}{144}=\frac{12(1+i)·4}{144}=\frac{48}{144}(1+i)=\frac{1}{3}(1+i)=\frac{\sqrt{2}}{3}(\cos \frac{\pi }{4}+i\sin \frac{\pi }{4})$

Biorr skrev:

Jag tror du försöker visa om man inte kan omvandla varje faktor i bråket till polär form, och ta sig vidare därifrån. Är det det du vill visa?

Svaret är att det blir nog väldigt komplicerat. Men så enkelt blir det med hjälp av den exponentiella representationen av ett komplext tal.

Nu måste du antingen traggla på lite, och träna på aritmetiken för den rektangulära formen. (Eller tjuvkika framåt i läroboken och kolla på lösningarna här ovan)

Jag ser vad du vill visa.

Och du gör det bra (tycker iallafall jag...)! Problemet är att det inte finns några trigonometriska samband som enkelt visar att man räkna sådär, före man känner till Eulers formel.