Polär form
 hejsan
hejsan
håller på med Polynomekvationer.
Behöver hjälp att komma igång med a)
ska man fokusera på en led i taget? Eulers formel?
Man brukar ansätta ett , höja upp med det efterfrågade och till sist identifiera värdena, tror jag.
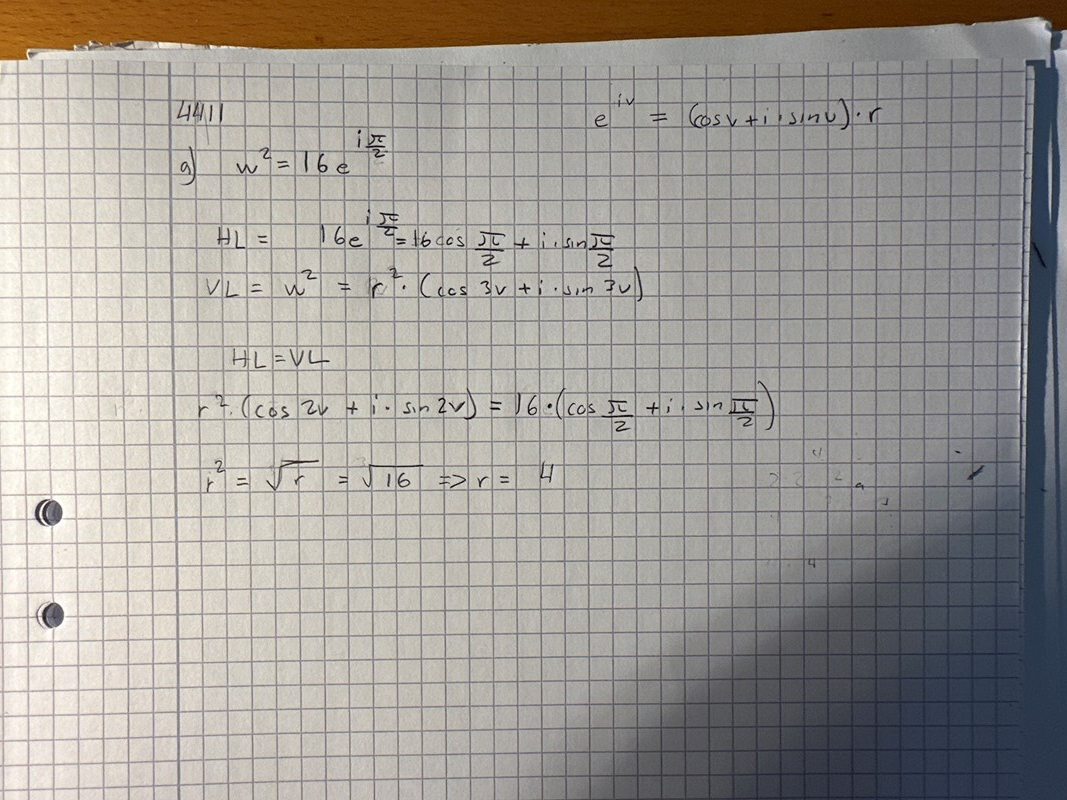 *korrigering
*korrigering
Det är lättare behålla det på formen .
 Kan min beräkning bli mer tydligt?
Kan min beräkning bli mer tydligt?
Biorr skrev:Kan min beräkning bli mer tydligt?
Jag tycker att den är tillräckligt tydlig.
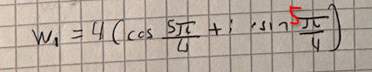
Jag tillämpar eulers formel för att omvandla HL till polär form
sedan omvandlar jag VL till polär form med hjälp av de Moivres formel.
sedan sätter jag VL=HL för att börja lösa ut r och vinklarna.
vinklarna erhålls genom ……grundekvation?…eller sedan så fortsätter jag med de Moivres formel för att få ut alla rötter? N=0, 1 ,2
Precis. Och när det blir fler rötter kan det vara fördelaktigt att markera dem i komplexa talplanet. Det är en bra kontroll.
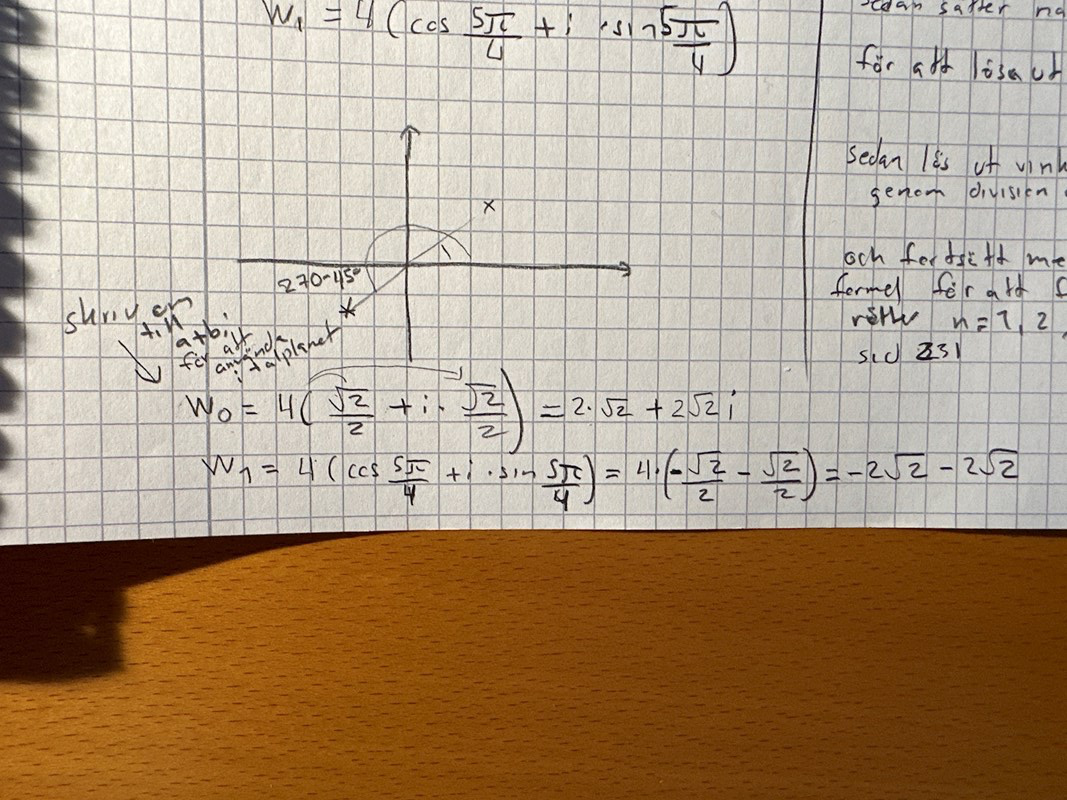 kan man markera dem i komplexa talplanet genom att omvandla w0 och w1 till rektangulära form?
kan man markera dem i komplexa talplanet genom att omvandla w0 och w1 till rektangulära form?
den ena blir i w0 ligger i den första kvadranten och w1 ligger i den tredje kvadranten.
men man får uppskatta, när miniräknare inte tillåts
Man får välja vilken form man vill. Det viktiga är att man via sin period inte lyckas nå fler lösningar. Nu var det en andragradsekvation så två rötter var väntat. Men om vi har en sjättegradare där vi kan vänta oss sex rötter så ska vi på ett varv kunna nå alla sex lösningar med en periods avstånd mellan varje.
Biorr skrev:kan man markera dem i komplexa talplanet genom att omvandla w0 och w1 till rektangulära form?
den ena blir i w0 ligger i den första kvadranten och w1 ligger i den tredje kvadranten.
men man får uppskatta, när miniräknare inte tillåts
Har man en gradskiva så är det inte så svårt. Markera vinklarna och sedan drar man en sträcka med rätt längd (bra om gradskivan har en "linjal").
På c)
 på c) skrev de bara z1 som svar
på c) skrev de bara z1 som svar
varför?
Biorr skrev:På c)
på c) skrev de bara z1 som svar
varför?
Det beror nog på att de har satt ut ±.


