Polära koordinater
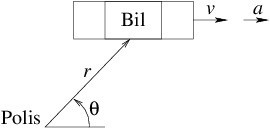
En bil kör förbi en polisradar.Beräkna beloppet av kraften som verkar på bilen (som har massan 771 kg) om polisen mäter = 5,08 m/s², en vinkelhastighet = −0,245 rad/s då bilen är på avståndet r = 59,33 m och vinkeln är θ = 42,54°
Jag vet inte hur jag ska beräkna ˙r, dvs m/s.
Jag vet hur jag ska lösa uppgiften, men jag vet inte hur jag ska ta fram r prim. Formeln för att ta fram accelerationen ser ut såhär.
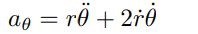
Man använder den dividerad med sinus vinkeln för att ta fram accelerationen a.
Jag är osäker på hur r punkt tas fram. Hade varit bra med lite vägledning. Testade med att ta radien multiplicerad med cos vinkeln men fick fel svar...
Kan du förklara (med ord) vad det är du försäker beräkna?
Visa spoiler
Kraften som verkar påbilen är proportionell mot accelerationen. Accelerationen (riktad rakt åt höger) är tidsderivatan av bilens hastighet v. Ta fram funktionen f(t) först!
helsai skrev:En bil kör förbi en polisradar. Beräkna beloppet av kraften som verkar på bilen (som har massan 771 kg) om polisen mäter = 5,08 m/s², en vinkelhastighet = −0,245 rad/s
Konstig uppgift. Varför skulle polisen hålla på med att mäta bilars acceleration?
Tänk på att både acceleration och hastighet är i x-riktningen, dvs hastighet och acceleration i y-led är noll. Du kan utnyttja detta.
Tex så måste vy = = 0. Notera att y = .
Pieter Kuiper skrev:helsai skrev:En bil kör förbi en polisradar. Beräkna beloppet av kraften som verkar på bilen (som har massan 771 kg) om polisen mäter = 5,08 m/s², en vinkelhastighet = −0,245 rad/s
Konstig uppgift. Varför skulle polisen hålla på med att mäta bilars acceleration?
Nya lagar från 1:a augusti?
PATENTERAMERA skrev:Tänk på att både acceleration och hastighet är i x-riktningen, dvs hastighet och acceleration i y-led är noll. Du kan utnyttja detta.
Tex så måste vy = = 0. Notera att y = .
Jag förstod tyvärr inte det du försöker säga. Men det jag måste ta reda på är r’.
0 = = = .
PATENTERAMERA skrev:0 = = = .
Någon fråga?
PATENTERAMERA skrev:Någon fråga?
Jag skrev vad är cot?
cotx = 1/tanx.
PATENTERAMERA skrev:cotx = 1/tanx.
Det bliri fel r värde när jag använder din formel.
r och ges i problemtexten, du behöver inte räkna ut dem.
PATENTERAMERA skrev:r och ges i problemtexten, du behöver inte räkna ut dem.
Jag får fel värde. Svaret på uppgiften är 1,59 kN.
Du får visa hur du räknat så vi kan se var det gått fel.
helsai skrev:Jag får fel värde. Svaret på uppgiften är 1,59 kN.
Om man googlar hittar man en liknande uppgift. Bilen är lite tyngre osv, men där ges facit som 22 kN.
PATENTERAMERA skrev:Du får visa hur du räknat så vi kan se var det gått fel.
De har enbart skrivit att rprim finns men hur man räknat visas inte.
PATENTERAMERA skrev:Du får visa hur du räknat så vi kan se var det gått fel.


Din lösning stämmer inte med problemtexten. Vinkelacceleration och är inte givna i problemet. Du verkar blandat ihop olika uppgifter.
PATENTERAMERA skrev:
Problemtexten är exakt samma men med olika värden. I den jag lösningen jag skickat hade inte heller rprim givet.
Det står att både är givna i det problemet. Men i det problem som du angav först så var dessa inte givna från början. Det blir skillnad om de är givna eller inte.
Jag är också helt förvirrad.
Är det accelerationen som är given eller är det ?
Vad är bilens massa?
r prim är inte givet, men i lösningen står det att det är givet. De har bara inte visat beräkningen för den. Därför undrar jag hur de löst r prim.
OK, med de data du får givet så kanske det är bättre att utnyttja i stället att
cos = .
Där
.
Då slipper vi tänka på vad r-prick skall vara.
Tillägg: 1 aug 2022 18:45
Denna approach ger i alla fall samma svar som facit.
PATENTERAMERA skrev:OK, med de data du får givet så kanske det är bättre att utnyttja i stället att
cos = .
Där
Vad är ? Då menar du att man tar ar / sin(x) då? för att ta reda på vad a är.
Då slipper vi tänka på vad r-prick skall vara.
Tillägg: 1 aug 2022 18:45
Denna approach ger i alla fall samma svar som facit.
= 5,08 m/s2, enligt problemtexten.
Du får a enligt a = .
Tillägg: 1 aug 2022 20:37
Det blir division med cos i stället för sin eftersom vi utnyttjar i stället för .
Nej, nu blev det konstigt.
eftersom restriktion i -led
Vad menar du med att det blev konstigt?
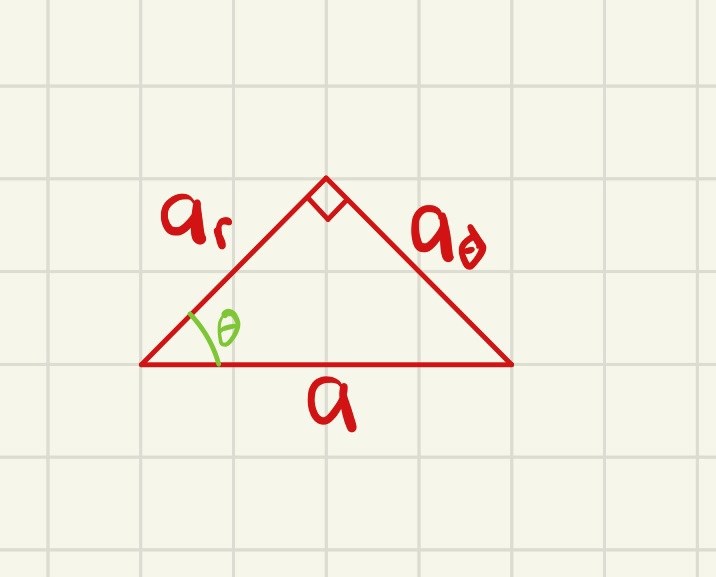
Uppgifterna givna i inlägg #19 är inte konsistenta. Menar du att du räknade på uppgifterna från det första inlägget?
Edit: Det var kanske så du menade, alltså och ja, det ger ju faktiskt "rätt" svar.
Ja, ursprungsproblemet. Tyckte var lite renare, men det blir ju samma. Möjligen skall det vara beloppstecken som du säger, men lite osäker här.
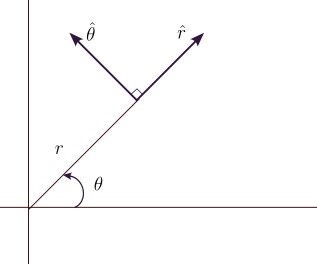 När vinkeln ökar moturs ges basvektorerna i polära koordinater av
När vinkeln ökar moturs ges basvektorerna i polära koordinater av
Vi noterar särskilt att samt .
Om vi deriverar lägesvektorn två gånger med avseende på tid får vi
Nu ger villkoret förhållandet mellan komponenterna
Vill man vara noga med tecknet gäller alltså
Mer specifikt ger villkoret
Vilket kan vara användbart om man saknar .
Slutligen är med riktning definierad av problemtextens figur. Absolutbeloppet indikerar bara att vi har förstörde teckeninformation under kvadreringen.
Precis, så måste det vara, och då får vi väl
, där vi utnyttjat D4ANIELS formel ovan för att få de två sista uttrycken.
Jag fick inte samma svar genom den du angav.
PATENTERAMERA skrev:
OK, med de data du får givet så kanske det är bättre att utnyttja i stället att
cos = .
Där
.
Då slipper vi tänka på vad r-prick skall vara.
HUr fick du rätt svar? Jag fick inte det.
Tillägg: 1 aug 2022 18:45
Denna approach ger i alla fall samma svar som facit.
1,59 kN.
Tillägg: 11 aug 2022 20:39
Se till att ha räknaren inställd på grader.