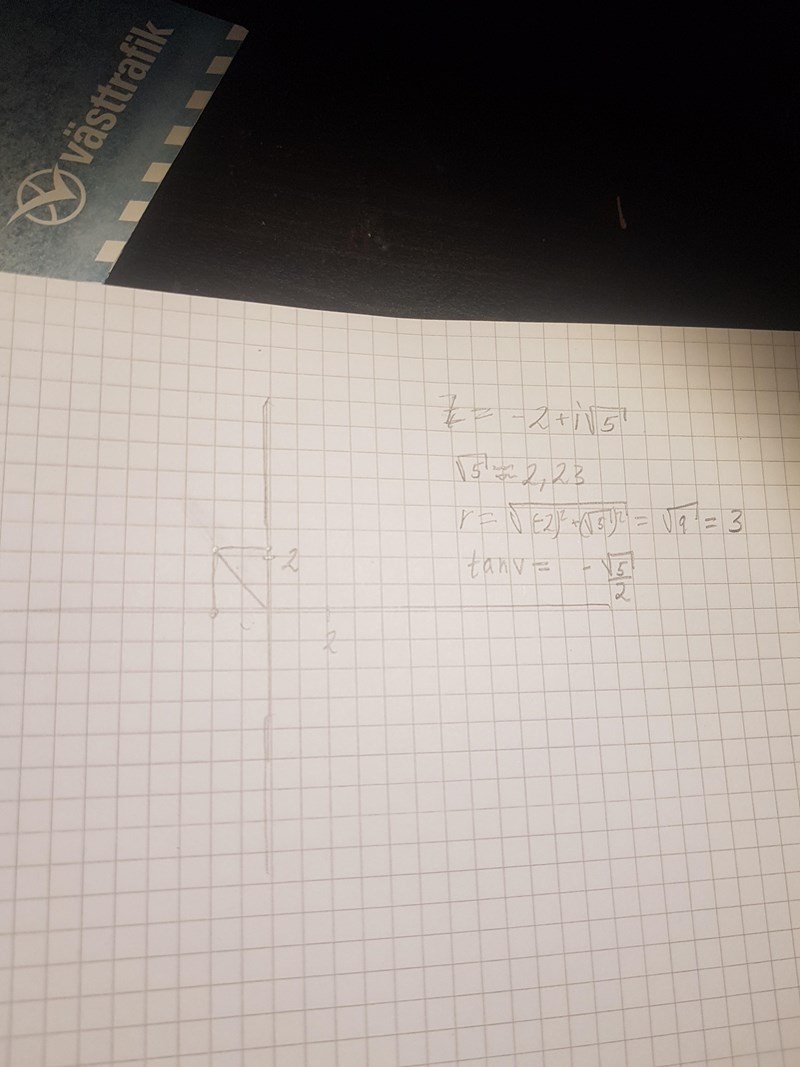Polärform och Potensform
Hej jag har fastnat på en uppgift i matte 4 där frågan går såhär "Skriv i polär from och potensform talet z= Jag vet hur jag ska räkna polärform men fattar inte potensform vilken formel ska jag använda och hur får jag svaret. Tack för svar.
Känner du till Eulers formel?
Ja, får arctan som svaret blir ungefär -48 grader sen omvandlar jag till radinaer som blir ungefär -0,84 och härifrån vet jag inte vad jag ska göra
Polär form kan du läsa om här:
https://www.matteboken.se/lektioner/matte-4/komplexa-tal/komplexa-tal-i-polar-form
Börja alltid med att rita ditt tal i ett koordinatsystem! Underlättar enormt när man ska bestämma argumentet!
Du behöver belopp och argument av -2 +i*sqrt(5)
Vad är beloppet?
Argumentet kan inte vara det du skrev, ditt tal ligger i tredje kvadranten.
Hej jag hade märkt att jag skrev frågan lite fel det ska stå som svaret blir ungefär -48 som sedan blir -0,84 i radianer. Har räknat ut absolutbeloppet . Men hur ska jag räkna det i potensform?
Beloppet är rätt, men argumentet är fortfarande fel. Rita en bild!
Det finns flera vinklar v i enhetscirkeln som har ett visst värde på tan(v).
Du är i andra kvadranten. Mellan vilka värden är argumentet?
ska jag inte ba ta arctan och få värden? För jag får ett negativt värde vilket är fel för den ligger i andra kvadranten.
master22 skrev:ska jag inte ba ta arctan och få värden? För jag får ett negativt värde vilket är fel för den ligger i andra kvadranten.
Hej.
Nej du kan inte bara göra så. Du måste dessutom använda din figur för att klura ut vad vinkeln ska vara.
Du har skrivit lite fel. Rottecknet ska bara vara över täljaren, minustecknet ska vara i nämnaren och den imaginära enheten ska inte vara med.
Om du tar , vilket är samma sak som så får du en vinkel som är ungefär -48°.
Hur förhåller sig denna vinkel till den du eftersöker?
Här är det viktigt att du tar hjälp av din figur.
Men är det rätt -48° för den ligger i andrakvadranten ska jag ta 180-48 eller?
master22 skrev:Men är det rätt -48° för den ligger i andrakvadranten ska jag ta 180-48 eller?
Ja. Fast du ska räkna i radianer. Och med exakta värden.
180° = och -48° är -0,84 är det så?
master22 skrev:180° = och -48° är -0,84 är det så?
Ja 180° är exakt radianer och -48° är ungefär -0.84 radianer.
Men jag tror att du ska svara med exakta vinklar.
Hur ska jag få det?
master22 skrev:Hur ska jag få det?
är en exakt vinkelangivelse.
Men kommer det inte bli svårt att skriva det på potensform isåfall hur?
master22 skrev:Men kommer det inte bli svårt att skriva det på potensform isåfall hur?
Det går utmärkt att skriva
eller
, där
Tack så mycket för att du har hjälpt mig och gav mig svaret
Yngve skrev:master22 skrev:Men kommer det inte bli svårt att skriva det på potensform isåfall hur?
Det går utmärkt att skriva
eller
, där
pi plus arctan... tycker jag.
Kan man ba skriva svaret så och få rätt z=
Hur definierar din bok "potensform"?
master22 skrev:Kan man ba skriva svaret så och få rätt z=
Ja nästan. Jag har sagt fel. Precis som Laguna skrev nyss så ska det vara pi PLUS arctan(...).
Kolla igen på din figur. Den vinkel du söker är ju pi radianer (ett halvt varv) större än den du får ut av arctan(...).
Alternativt om du inte vill ha negativt argument till arctan:
master22 skrev:
Man brukar kalla de olika formerna för komplexa tal så här:
- Rektangulär form:
- Trigonometrisk polär form:
- Exponentiell polär form:
så blir detta svaret till slut?
master22 skrev:så blir detta svaret till slut?
Ja (förutom att det saknas en avslutande parentes i exponenten).
Eller
så de här har samt värde och spelar ingen roll vilken jag svarar?
master22 skrev:så de här har samt värde och spelar ingen roll vilken jag svarar?
Det stämmer. Men du kan och bör kontrollera det själv genom att beräkna de två argumenten med räknaren.